May 27th, 2021

We simulate the modified KB10 model (perhaps we will call it the $\beta$-null regime of the KB10 model) and find parameters that appear to admit traveling pulse solutions. We analyzed equations 3.30-3.31 from Kilpatrick & Bressloff 2010 in this case, but they appear inconsistent with observations. Perhaps the assumption that $\beta \ne 0$ was essential in their derivation. We may have to re-derive the traveling-pulse solution from scratch.

To-Do List Snapshot

Modified KB10 Simulation

What we are calling the modifed KB10 model is the model from Kilpatrick & Bressloff 2010 (KB10) but with the synaptic depression ($q$) removed. This is equivalent to setting $\beta = 0$ and initializing $q = 1$ in their model. The result is then $$\begin{align*} \mu u_t &= -u + \int_{-\infty}^\infty w(x,x^\prime) f( u(x^\prime,t) - a(x^\prime,t)) \ dx^\prime \\ \alpha a_t &= -a + \gamma f(u - a). \end{align*}$$ Note that we have re-labeled the parameters $\epsilon \to \alpha$ and the old $\alpha$ is not present.

With the removal of the synaptic depression variable, we will need to find new parameter-sets that admit traveling wave solutions. In particular, in KB10 with their choice of parameters, the synaptic depression appeared to be the primary restorative force, with hyperpolarizing adaptation current ($a$) playing a minor role. With our removal of the synaptic depression we will need to tune the parameters so that the hyperpolarizing adaptation current can provide sufficient restoration. This suggests increasing $\gamma$. Below, Figure 1 does exactly this and we indeed have a traveling pulse.

Fig 1. The modified KB10 model with $w(x,y) = \frac{1}{2}e^{-|x-y|}$, $f(u) = H(u-\theta)$, and parameters: $\theta = 0.1, \alpha = 5, \gamma = 1, \mu = 1$. The initial condition is $a=0$ and $u$ is a cosine bell with height 1 and width 50. The pulse-width here is approximately $\Delta = 38.83$ (the measure of $\{x : J(x)>\theta\}$) and the pulse-speed is approximately $c=3.924$. (simulation code [notebook download])

Figure 2 (below) shows the same parameter choices, but with the initial conditions set to create two pulses traveling in opposite directions. As predicted, they simply annihilate eachother. Since the traveling pulse solutions to the modified KB10 model are unique (as it is a special case of the KB10 model) there are essentially no other configurations to test. I don't think that there is anything interesting to study for colliding pulses in one dimension.

Fig 2. The modified KB10 model with $w(x,y) = \frac{1}{2}e^{-|x-y|}$, $f(u) = H(u-\theta)$, and parameters: $\theta = 0.1, \alpha = 5, \gamma = 1, \mu = 1$. The initial condition is $a=0$ and $u$ is a sum of cosine bells with height 1 and width 50 and centers $x=0, 500$. The traveling pulses of opposite direction annihilate. (simulation code [notebook download])

Traveling Pulse Solutions

Since we are working with a special case of the KB10 model, should be able to re-use the analysis from Kilpatrick & Bressloff 2010. In particular, their Equations 3.30-31 give that our wave speed $c$ and pulse width $\Delta$ are given as the solution to the following system (derivation below) $$\begin{align*} \Delta &= \log{\left(\frac{1}{- 2 \theta \left(c + 1\right) + 1} \right)}\\ 0 &= \gamma \left(\left(- 2 \theta \left(c + 1\right) + 1\right)^{\frac{\alpha}{c}} - 1\right) + \frac{- 2 \theta c + c^{2} \left(- 2 \theta - \left(- 2 \theta \left(c + 1\right) + 1\right)^{\frac{1}{c}} + 1\right)}{c^{2} - 1}. \end{align*}$$

We begin with $$\begin{align*} 0 &= K_{0} - K_{1} e^{- \Delta} - K_{2} e^{- \Delta} e^{\frac{\Delta \left(- \alpha \beta - 1\right)}{\alpha c}} - \theta\\ 0 &= L_{0} + L_{1} e^{- \Delta} + L_{2} e^{\frac{\Delta \left(- \alpha \beta - 1\right)}{\alpha c}} - L_{3} e^{- \frac{\Delta}{c}} + \gamma e^{- \frac{\Delta}{\epsilon c}} - \theta\\ K_{0} &= \frac{\alpha c + 1}{\left(2 c + 2\right) \left(\alpha \beta + \alpha c + 1\right)}\\ K_{1} &= \frac{1}{\left(2 c + 2\right) \left(\alpha \beta + 1\right)}\\ K_{2} &= \frac{\alpha^{2} \beta c}{\left(2 c + 2\right) \left(\alpha \beta + 1\right) \left(\alpha \beta + \alpha c + 1\right)}\\ L_{0} &= - \gamma + \frac{c + \frac{1}{2}}{\left(c + 1\right) \left(\alpha \beta + 1\right)}\\ L_{1} &= \frac{\alpha c - 1}{\left(2 c - 2\right) \left(- \alpha \beta + \alpha c - 1\right)}\\ L_{2} &= \frac{\alpha^{4} \beta c^{2}}{\left(\alpha \beta + 1\right) \left(\alpha^{2} c^{2} - \left(\alpha \beta + 1\right)^{2}\right) \left(- \alpha \beta + \alpha - 1\right)} - \frac{\alpha^{2} \beta c}{2 \left(c + 1\right) \left(\alpha \beta + 1\right) \left(\alpha \beta + \alpha c + 1\right)}\\ L_{3} &= \frac{\frac{\alpha^{4} \beta c^{2}}{\left(\alpha^{2} c^{2} - \left(\alpha \beta + 1\right)^{2}\right) \left(- \alpha \beta + \alpha - 1\right)} + 1}{\alpha \beta + 1} + \frac{\alpha^{2} c^{2} \left(\beta + 1\right) - \alpha \beta - 1}{\left(c^{2} - 1\right) \left(\alpha^{2} c^{2} - \left(\alpha \beta + 1\right)^{2}\right)}. \end{align*}$$ Then set $\beta=0$ to obtain $$\begin{align*} 0 &= K_{0} - K_{1} e^{- \Delta} - K_{2} e^{- \Delta} e^{- \frac{\Delta}{\alpha c}} - \theta\\ 0 &= L_{0} + L_{1} e^{- \Delta} + L_{2} e^{- \frac{\Delta}{\alpha c}} - L_{3} e^{- \frac{\Delta}{c}} + \gamma e^{- \frac{\Delta}{\epsilon c}} - \theta\\ K_{0} &= \frac{1}{2 \left(c + 1\right)}\\ K_{1} &= \frac{1}{2 c + 2}\\ K_{2} &= 0\\ L_{0} &= - \gamma + \frac{c + \frac{1}{2}}{c + 1}\\ L_{1} &= \frac{1}{2 c - 2}\\ L_{2} &= 0\\ L_{3} &= 1 + \frac{1}{c^{2} - 1}. \end{align*}$$ Substituting, we find $$\begin{align*} 0 &= - \theta - \frac{e^{- \Delta}}{2 c + 2} + \frac{1}{2 \left(c + 1\right)}\\ 0 &= \gamma \left(-1 + e^{- \frac{\Delta}{\epsilon c}}\right) - \theta + \frac{c}{c + 1} - e^{- \frac{\Delta}{c}} - \frac{1}{c^{2} e^{\frac{\Delta}{c}} - e^{\frac{\Delta}{c}}} + \frac{e^{- \Delta}}{2 c - 2} + \frac{1}{2 \left(c + 1\right)}. \end{align*}$$ Solving the first equation for $e^{-\Delta}$ and substituting, we obtain $$\begin{align*} e^{- \Delta} &= - 2 \theta c - 2 \theta + 1\\ 0 &= \gamma \left(\left(- 2 \theta c - 2 \theta + 1\right)^{\frac{1}{\epsilon c}} - 1\right) - \theta + \frac{c}{c + 1} - \left(- 2 \theta c - 2 \theta + 1\right)^{\frac{1}{c}} - \frac{1}{c^{2} \left(- 2 \theta c - 2 \theta + 1\right)^{- \frac{1}{c}} - \left(- 2 \theta c - 2 \theta + 1\right)^{- \frac{1}{c}}} + \frac{- 2 \theta c - 2 \theta + 1}{2 c - 2} + \frac{1}{2 \left(c + 1\right)}. \end{align*}$$ Rearranging, we arrive at a one-dimensional root finding problem for $c$, and some simple substitution for $\Delta$ $$\begin{align*} \Delta &= \log{\left(\frac{1}{- 2 \theta \left(c + 1\right) + 1} \right)}\\ 0 &= \gamma \left(\left(- 2 \theta \left(c + 1\right) + 1\right)^{\frac{1}{\epsilon c}} - 1\right) + \frac{- 2 \theta c + c^{2} \left(- 2 \theta - \left(- 2 \theta \left(c + 1\right) + 1\right)^{\frac{1}{c}} + 1\right)}{c^{2} - 1}. \end{align*}$$ Converting to our parameter naming conventions $\epsilon \to 1/\alpha$ we have $$\begin{align*} \Delta &= \log{\left(\frac{1}{- 2 \theta \left(c + 1\right) + 1} \right)}\\ 0 &= \gamma \left(\left(- 2 \theta \left(c + 1\right) + 1\right)^{\frac{\alpha}{c}} - 1\right) + \frac{- 2 \theta c + c^{2} \left(- 2 \theta - \left(- 2 \theta \left(c + 1\right) + 1\right)^{\frac{1}{c}} + 1\right)}{c^{2} - 1}. \end{align*}$$

(code [notebook download])

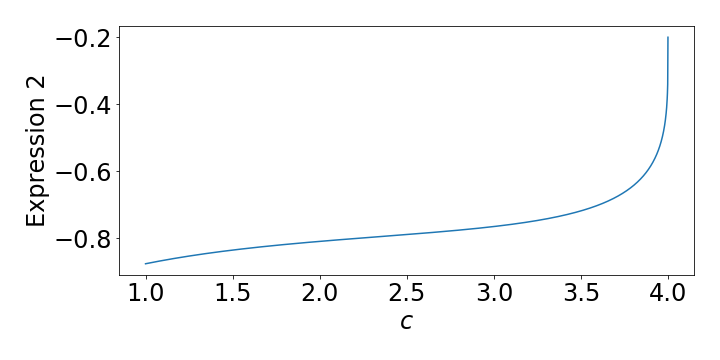
In order for $c$ and $\Delta$ to be real-valued, we require $c < \frac{1}{2\theta} - 1$. For our choice of parameters in the simulations above ($\gamma = 1, \theta = 0.1$) this suggests a maximum speed of $c_\text{max} = 4$. Unfortunatley, rootfinding attempts have been unsuccessful. Figure 3 below, shows a plot of the RHS of our expression, for which we seek a root. It appears that the function is bounded above by $-0.2$ and thus no root can exisit. This seems at odds with our simulation.

Fig 3.The RHS of the second equation, as a function of $c$ with parameters given by $\gamma = 1, \theta=0.1, \alpha=5$. We can see that the expression is bounded above by $-0.2$ and thus our system is not consistent. (code [notebook download])

For reference, here is the generated code for the function depicted in Figure 3, above. 

def c_implicit(c, γ, α, θ=0.1):
    return γ*(( lambda base, exponent: base**exponent )(-2*θ*(c + 1) + 1, α/c) - 1) + (-2*θ*c + ( lambda base, exponent: base**exponent )(c, 2)*(-2*θ - ( lambda base, exponent: base**exponent )(-2*θ*(c + 1) + 1, 1.0/c) + 1))/(( lambda base, exponent: base**exponent )(c, 2) - 1)