Sage Shaw - Mathematician / Data scientist

Open to work!
I’m looking for a Data Scientist position. Take a look at my resume to see if I would be a good fit for your company or organization. If you’re interested in hiring me, send me an email!
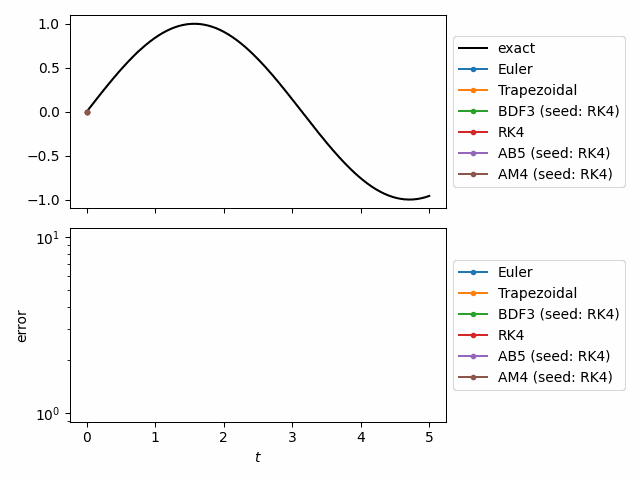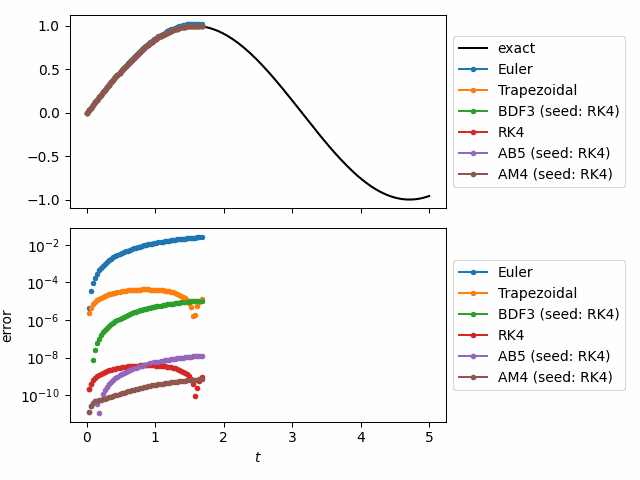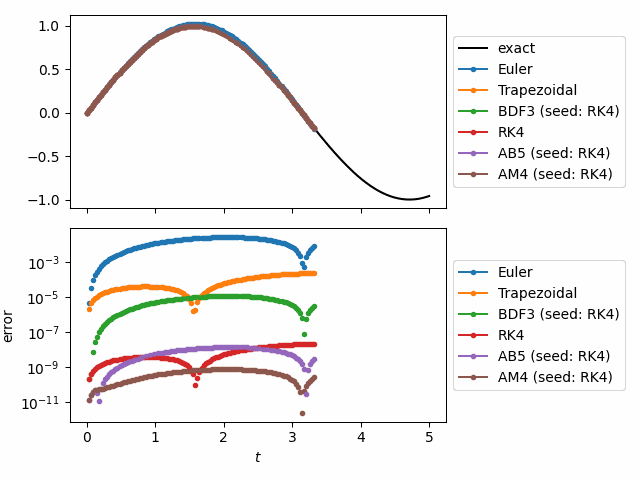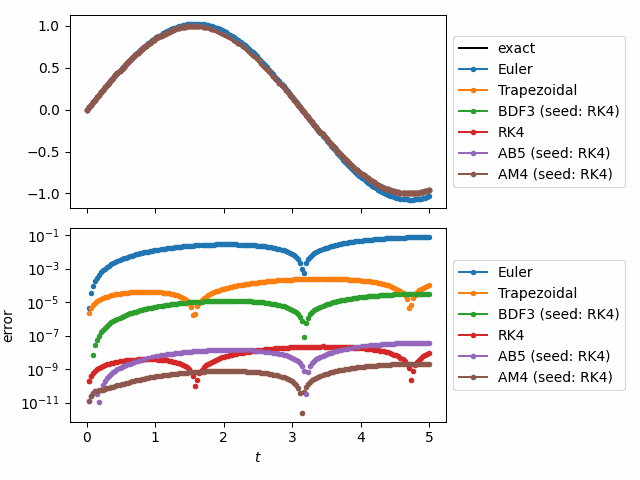
My package odeiter now has documentation
odeiter is a python package for solving systems of differential equations using generators. Generators decouple the iteration from the looping body. This allows you to loop over the solution directly, and separates the solve code (handled by odeiter) from the code you write to do something productive with the solution.