$ \newcommand{\RR}{\mathbb{R}} \newcommand{\NN}{\mathbb{N}} \newcommand{\OO}{\mathcal{O}} \newcommand{\mathcow}{\OO} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\CC}{\mathbb{C}} \newcommand{\KK}{\mathbb{K}} \newcommand{\PP}{\mathcal{P}} \newcommand{\TT}{\mathcal{T}} \newcommand{\BB}{\mathcal{B}} \newcommand{\LL}{\mathcal{L}} \renewcommand{\Re}{\operatorname{Re}} \renewcommand{\Im}{\operatorname{Im}} \newcommand{\veca}{\vec{a}} \newcommand{\vecb}{\vec{b}} \newcommand{\vecd}{\vec{d}} \newcommand{\vece}{\vec{e}} \newcommand{\vecf}{\vec{f}} \newcommand{\vecn}{\vec{n}} \newcommand{\vecp}{\vec{p}} \newcommand{\vecr}{\vec{r}} \newcommand{\vecu}{\vec{u}} \newcommand{\vecv}{\vec{v}} \newcommand{\vecx}{\vec{x}} \newcommand{\vecy}{\vec{y}} \newcommand{\vecz}{\vec{z}} \renewcommand{\vec}[1]{\mathbf{#1}} $ Shaw Research Notes

July 29th, 2021

We attempt to identify difficulties in convergence of the numerical scheme. Discontinuity of the forcing term makes this a difficult task. In particular, that the forcing term is not Lipshitz continuous precludes applying most related theorems. We add detail to the previously suggested algorithm and now have a working cusp-detection implementation.

To-Do List Snapshot

Non-convergence

Previous observations have lead us to suspect that Euler's method using the semi-analytic convolution is not convergent for the adaptive model. To motivate this, we have performed a more direct test of convergence traveling wave solution (using parameters $\mu= 1, \alpha = 5, \gamma= 1, \theta= 0.1$) advanced to $t_f = 10$. Figures 1, 2, and 3 show the results, and suggest convergence, though sub-linear when measured in the $\infty$-norm. This is by no means certain, as the measured "order of convergence" slightly decreases as the mesh/step size decreases.

Fig 1. Convergence of the $u$ solution as $h \to 0$.
Fig 2. Convergence of the $u$ solution as $k \to 0$.
Fig 3. Convergence of the $u$ solution as $h=k \to 0$.

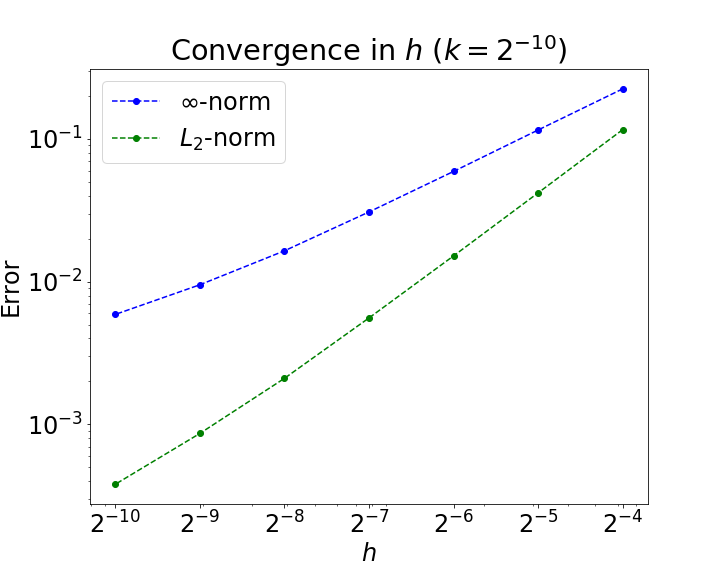
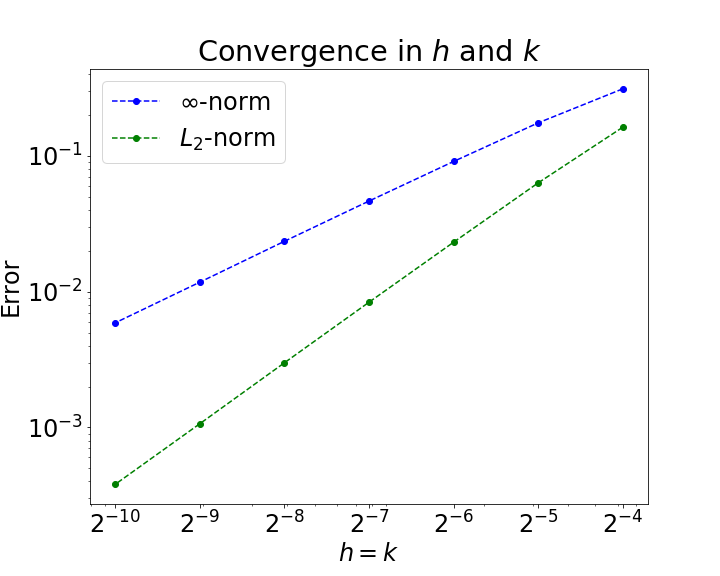
These results are somewhat perplexing. The original data that suggested non-convergence was measuring the speed of the pulse by way of the fore and aft threshold-crossings. Since the solution is continuous, error in the position of the threshold crossings would be related to the error at the true threshold-crossings by way of the Lipschitz constants at those points. Since the error at any particular point is bounded by the $\infty$-norm error, this would be the natural comparison.

Ideally, we would like a theorem to guarantee such convergence. However, we doubt a general theorem has been proven. In particular, discontinuity of the forcing term precludes Lipschitz continuity in $(u,a)$ and thus uniqueness of solutions is not guaranteed in general. This paper by John Hubbard et al. suggests that convergence using Euler's method isn't necessarily evidence for uniqueness of solutions.

Theorems from textbooks (for example Iserles 2012) often prove convergence of Euler's method assuming the forcing function is $C^2$ and citing Taylor's Theorem. However, the error bound can be written in terms of the Lipschitz constant, rather than a higher derivative. This Stack Exchange post outlines a proof of convergence with purportedly weaker conditions, though those conditions are not clearly stated. This is good news for the non-adaptive model. For the adaptive model, we may need to prove uniqueness of solutions and convergence of Euler's method ourselves.

Algorithm and Implementation Update

The update for $u$ is computationally comparable to updating $u$ in the non-adaptive model. Since the numerics appear sufficient in the non-adaptive model, a simple forward-Euler update for $u$ should be sufficient in the adaptive model. The improvements we develop for stepping the $a$ variable will mostly likely lead to improvements in updating $u$ as well, but let us set this aside for now.

The ODE governing $a$ is given by $$ \alpha a_t = -a + \gamma H(u - a - \theta) $$ and thus $a$ has a discontinuous derivative. Let $c_i(t)$ denote the position of the $i$th threshold-crossing at time $t$. Then $c_i'(t) = \frac{-J_t}{J_x} \bigg|_{x,t = c_i(t), t}$ where $J = u - a$. We can then approximate the non-linearity by $$ H(u - a - \theta) \approx \sum_{i} H \big( x - c_i(t_0) - c_i'(t_0) t \big) $$ allowing us to integrate analytically.

This requires approximating front locations and calculating $J_x$. Special care must be taken in the calculation of $J_x$ as $J$ has cusps where the derivative is discontinuous.

Presently, we have a working cusp-detection code that requires a bound on the 2nd derivative. The larger this bound, the smaller the mesh size must be in order for the detector to work. For our application, this should be sufficient, as $h \to 0$ and the traveling wave solution has a bounded second derivative.