July 7^th, 2021

Derived the wave-response approximation for a spatially localized delta pulse stimulus, and compared to simulations. Prepared for the July 8^th presentation to the research group.

To-Do List Snapshot

• Investigate wave-response function.
• Convert to a semi-analytic implementation.
• Spatially homogeneous pulse.
• Spatially homogeneous, temporally finite.
• Local pulses.
• Wave-train Analysis
• Search the literature.
• Find periodic solutions.
• Compare frequency to a pair of pulses.
• Reading
• Coombes 2004.
• Folias & Bressloff 2005.
• Faye & Kilpatrick 2018.

Spatially Localized Pulse

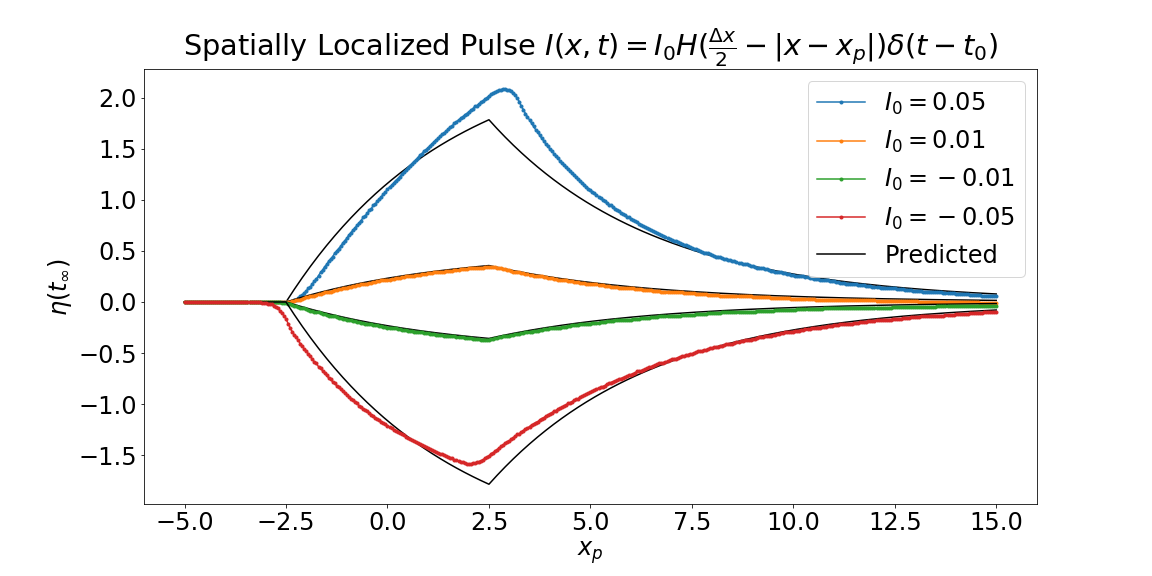
Here we explore the wave response to a spatially localized pulse stimulus $$I(x,t) = I_0 H(\tfrac{\Delta x}{2} - |x - x_p|) \delta(t-t_0)$$ where $t_0$ denotes the time of the pulse, $x_p$ denotes the location of the center of the pulse (relative to the front of the pulse at $x=0$), and $\Delta x$ denotes the width of the pulse.

For $t_0 = 0$ the adjoint method gives the first order asymptotic approximation to the wave response function as $$\eta(t) \approx \frac{\mu c + 1}{\mu \theta} I_0 \begin{cases} 0, & x_p \le - \tfrac{\Delta x}{2} \\ 1 - \exp \left( \frac{-(x_p + \tfrac{\Delta x}{2})}{c\mu} \right), & - \tfrac{\Delta x}{2} \le x_p < \tfrac{\Delta x}{2} \\ \exp \left( \frac{-(x_p - \tfrac{\Delta x}{2})}{c\mu} \right) - \exp \left( \frac{-(x_p + \tfrac{\Delta x}{2})}{c\mu} \right), & \tfrac{\Delta x}{2} \le x_p. \end{cases}$$

Figure 1 below shows our predicted wave response compared to simulation.

Fig 1. Wave response to the spatially localized pulse stimulus $I(x,t) = I_0 H(\tfrac{\Delta x}{2} - |x - x_p|) \delta(t-t_0)$. Here, $x_p$ denotes the center of the stimulated region and $\Delta x = 5$ denotes the width of the stimulated region.