Publications
Approximating the effect of inputs and cortical geometry on wave propagation in neural fields
PhD Thesis (2025)
My doctoral research focused on neural-field equations. These are integro-differential equations (similar to PDEs) that are useful for modeling neural activity at the tissue level. My dissertation is comprised of two parts.
The first part explores the dynamics of a specific neural field model that incorporates synaptic depression. This enables the model to support traveling pulse solutions and we explore the possibility of using these traveling pulses to encode the position of moving stimuli. The model successfully captures the apparent motion illusion - a phenomenon where a sequence of stationary stimuli is interpreted as a single moving object.
In the second part I analyse an algorithm for approximating solutions to neural field equations on realistic cortical surfaces. The algorithm uses radial basis function quadrature to approximate the spatial operator in the equations. Here is an example simulation on a realistic cortical surface.
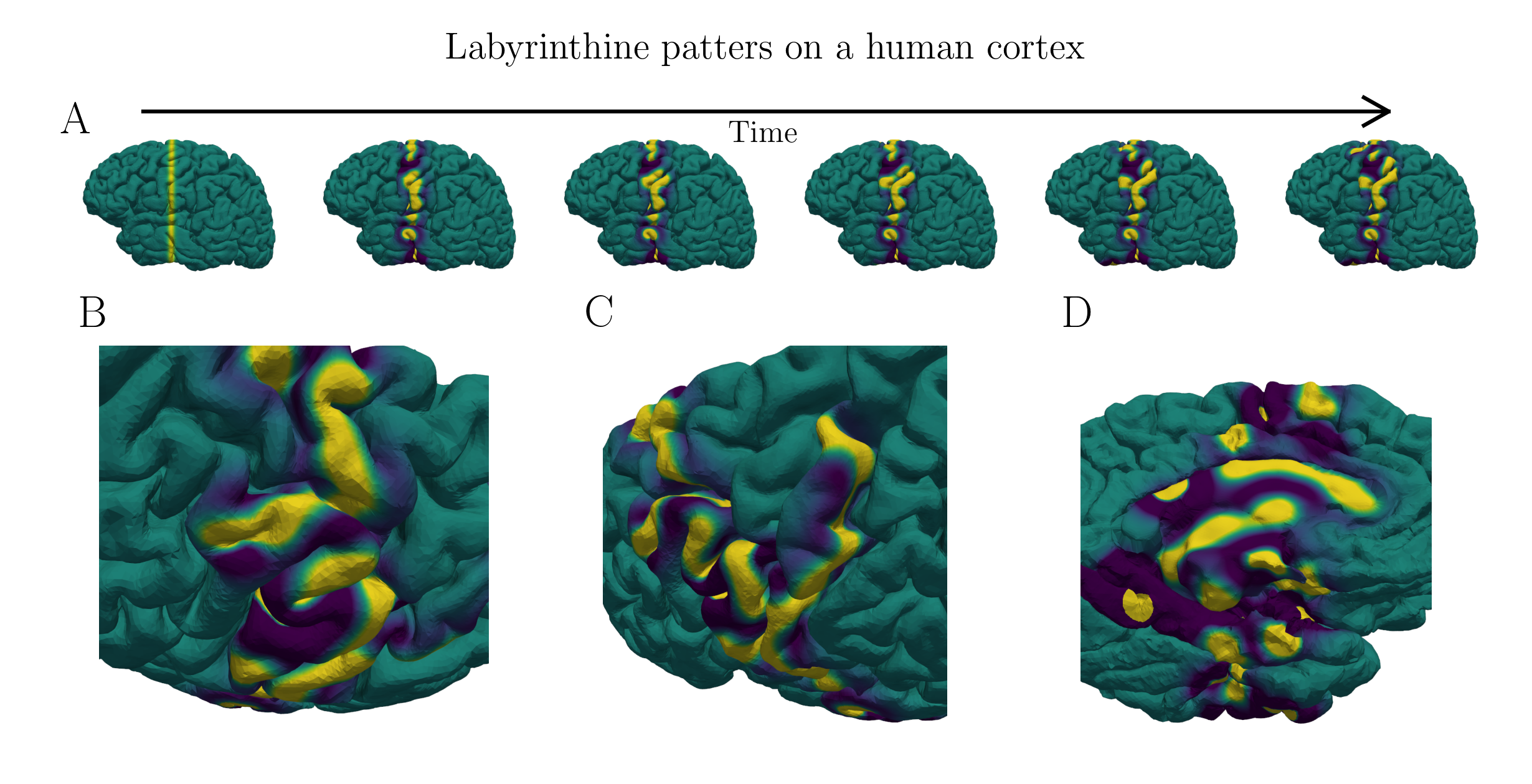
Radial Basis Function Techniques for Neural Field Models on Surfaces
ArXiv (2025) (submitted to SISC)
We present a numerical framework for solving neural field equations on surfaces using Radial Basis Function (RBF) interpolation and quadrature. Neural field models describe the evolution of macroscopic brain activity, but modeling studies often overlook the complex geometry of curved cortical domains. Traditional numerical methods, such as finite element or spectral methods, can be computationally expensive and challenging to implement on irregular domains. In contrast, RBF-based methods provide a flexible alternative by offering interpolation and quadrature schemes that efficiently handle arbitrary geometries with high-order accuracy. We first develop an RBF-based interpolatory projection framework for neural field models on general surfaces. Quadrature for both flat and curved domains are derived in detail, ensuring high-order accuracy and stability as they depend on RBF hyper-parameters (basis functions, augmenting polynomials, and stencil size). Through numerical experiments, we demonstrate the convergence of our method, highlighting its advantages over traditional approaches in terms of flexibility and accuracy. We conclude with an exposition of numerical simulations of spatiotemporal activity on complex surfaces, illustrating the method’s ability to capture complex wave propagation patterns.
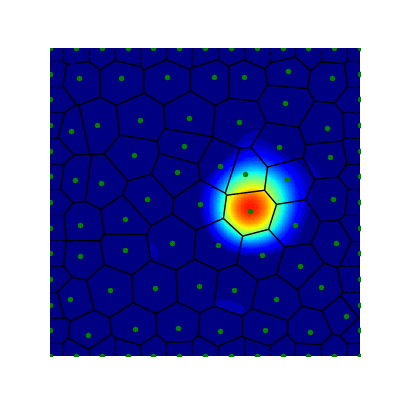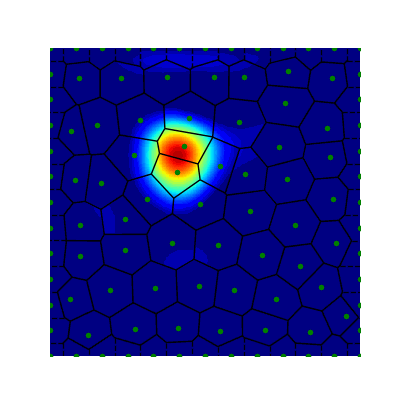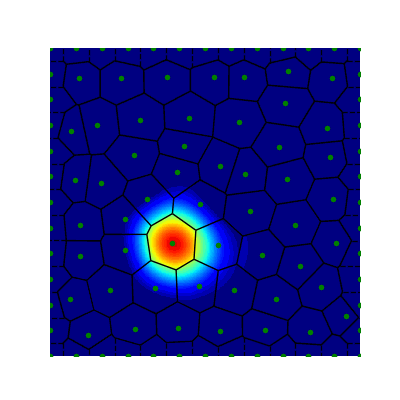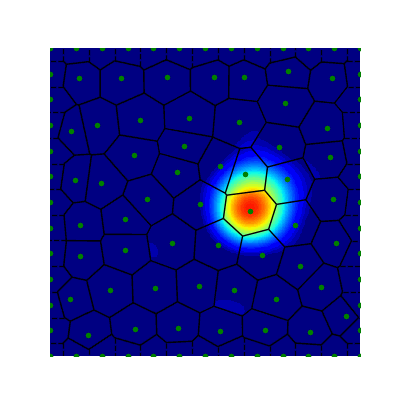
Representing stimulus motion with waves in adaptive neural fields
Journal of Computational Neuroscience(2024)
Traveling waves of neural activity emerge in cortical networks both spontaneously and in response to stimuli. The spatio-temporal structure of waves can indicate the information they encode and the physiological processes that sustain them. Here, we investigate the stimulus-response relationships of traveling waves emerging in adaptive neural fields as a model of visual motion processing. Neural field equations model the activity of cortical tissue as a continuum excitable medium, and adaptive processes provide negative feedback, generating localized activity patterns. Synaptic connectivity in our model is described by an integral kernel that weakens dynamically due to activity-dependent synaptic depression, leading to marginally stable traveling fronts (with attenuated backs) or pulses of a fixed speed. Our analysis quantifies how weak stimuli shift the relative position of these waves over time, characterized by a wave response function we obtain perturbatively. Persistent and continuously visible stimuli model moving visual objects. Intermittent flashes that hop across visual space can produce the experience of smooth apparent visual motion. Entrainment of waves to both kinds of moving stimuli are well characterized by our theory and numerical simulations, providing a mechanistic description of the perception of visual motion.
Radial Basis Function Finite Difference Approximations of the Laplace-Beltrami Operator
Partial differential equations (PDEs) are used throughout science and engineering for modeling various phenomena. Solutions to PDEs cannot generally be represented analytically, and therefore must be approximated using numerical techniques; this is especially true for geometrically complex domains. Radial basis function generated finite differences (RBF-FD) is a recently developed mesh-free method for numerically solving PDEs that is robust, accurate, computationally efficient, and geometrically flexible. In the past seven years, RBF-FD methods have been developed for solving PDEs on surfaces, which have applications in biology, chemistry, geophysics, and computer graphics. These methods are advantageous, as they are mesh-free, operate on arbitrary configurations of points, and do not introduce artificial singularities, as surface parameterizations are known to do. In this thesis, we develop a new RBF-FD method that uses projections on the tangent plane to approximate the Laplace-Beltrami operator (surface Laplacian). We then compare this method to two other previously developed RBF-FD methods: the Projected Gradient method and the Hermite RBF-FD method, on a set of benchmark problems posed on the sphere and torus. We also provide guidelines for choosing the various parameters involved in the methods.