Group Update - June 7^th, 2023

Sage Shaw - CU Boulder

Neural field Model with synaptic depression.

\begin{align*} \tau_u u' &= -u + w \ast (qf[u]) \\ \tau_q q' &= 1 - q - \beta q f[u] \end{align*}

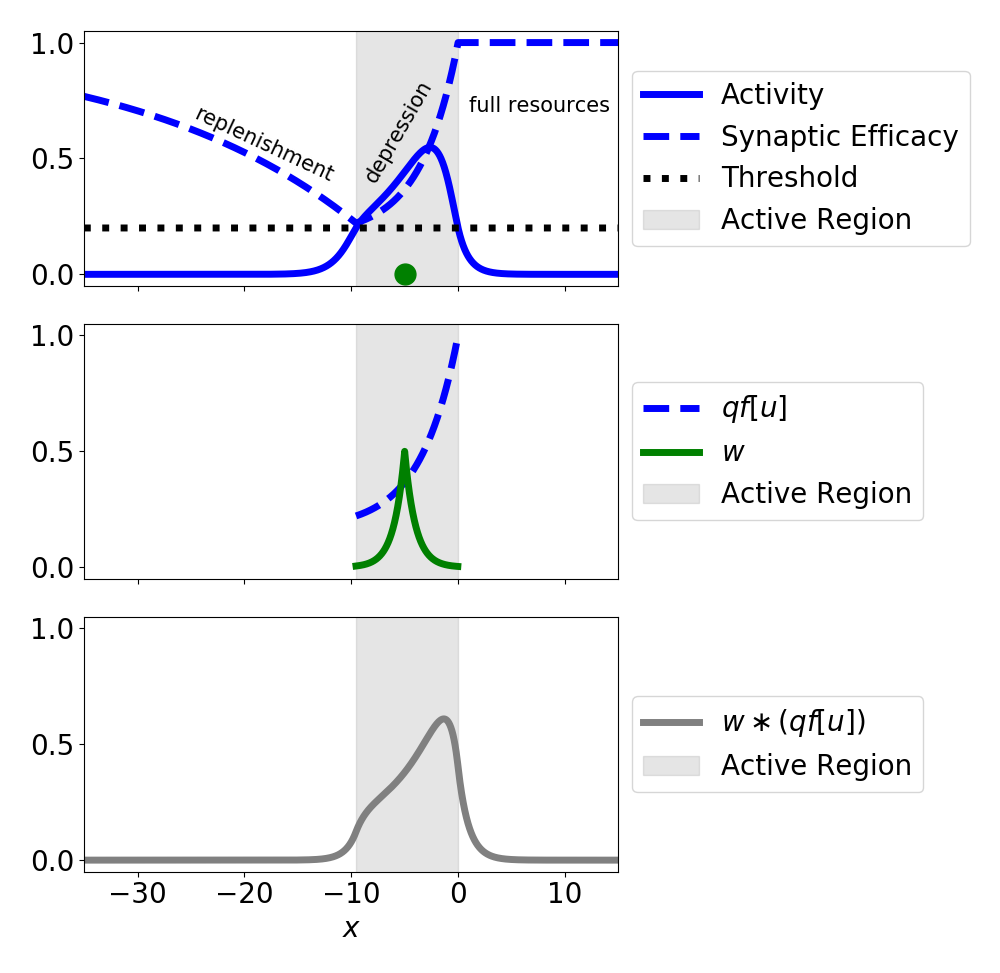
Marginally Stable Solutions

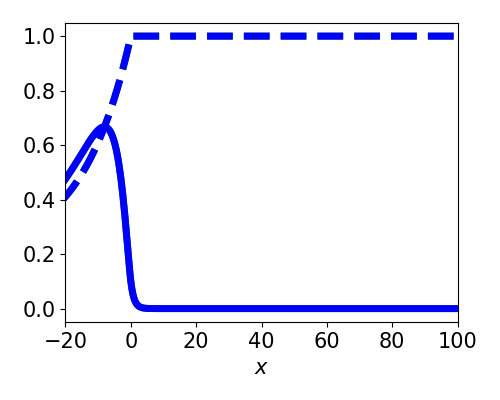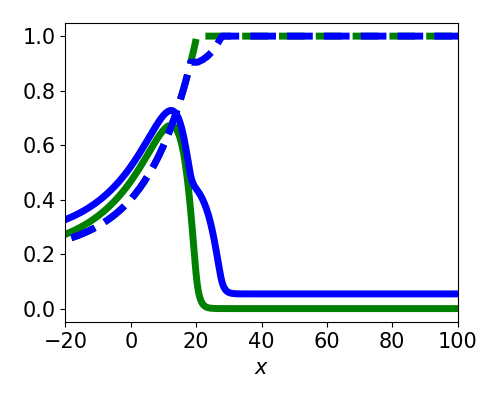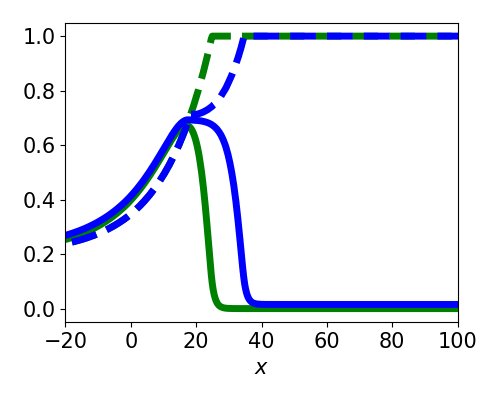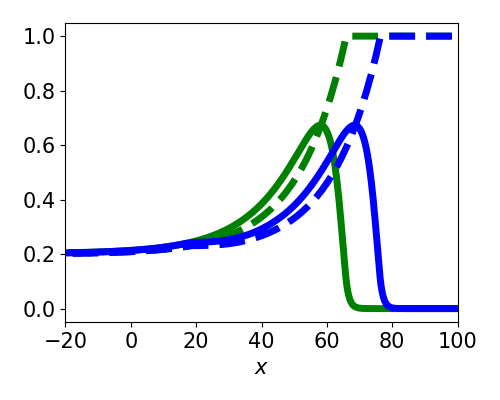
Asymptotic approximation to the wave response. $$ \nu' = -\frac{\langle v_1, I_u(\xi, t) \rangle + \langle v_2, I_q(\xi, t) \rangle}{\tau_u \langle v_1, U' \rangle + \tau_q \langle v_2, Q' \rangle} $$

Entrainment can't be predicted with this formula.

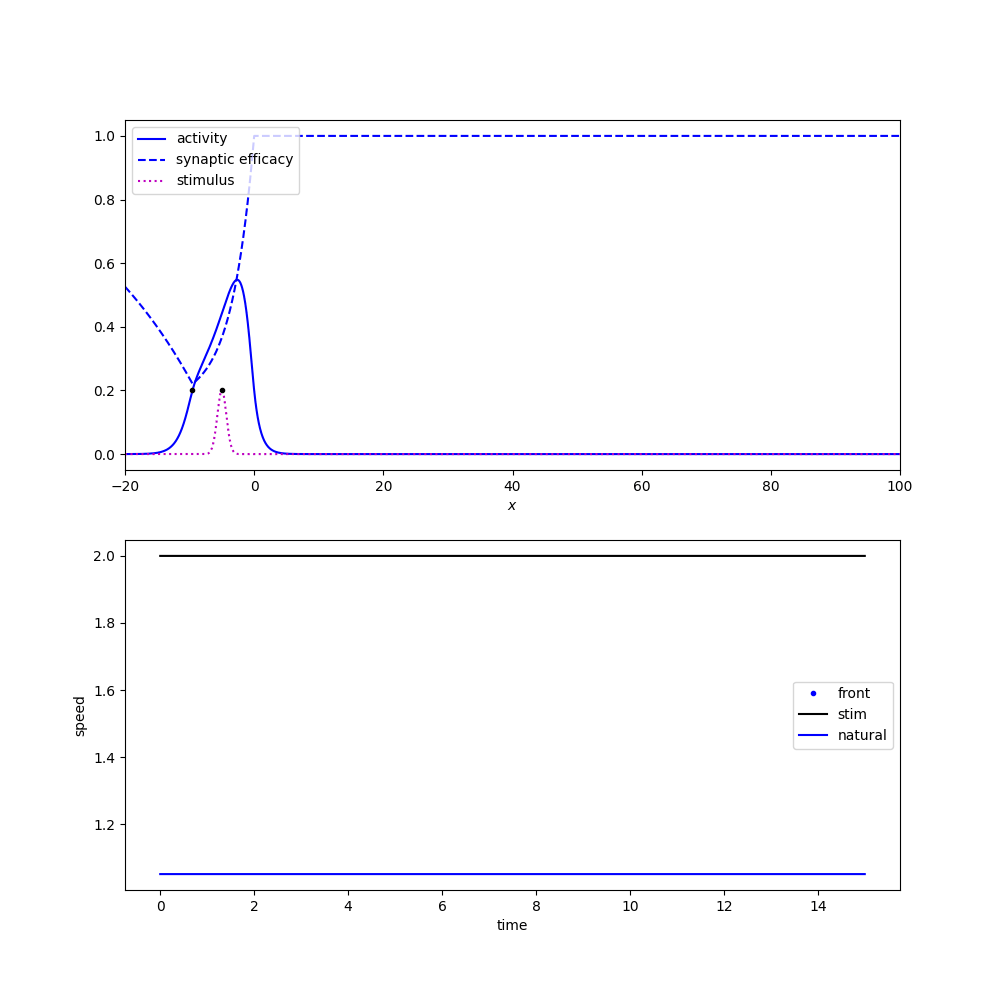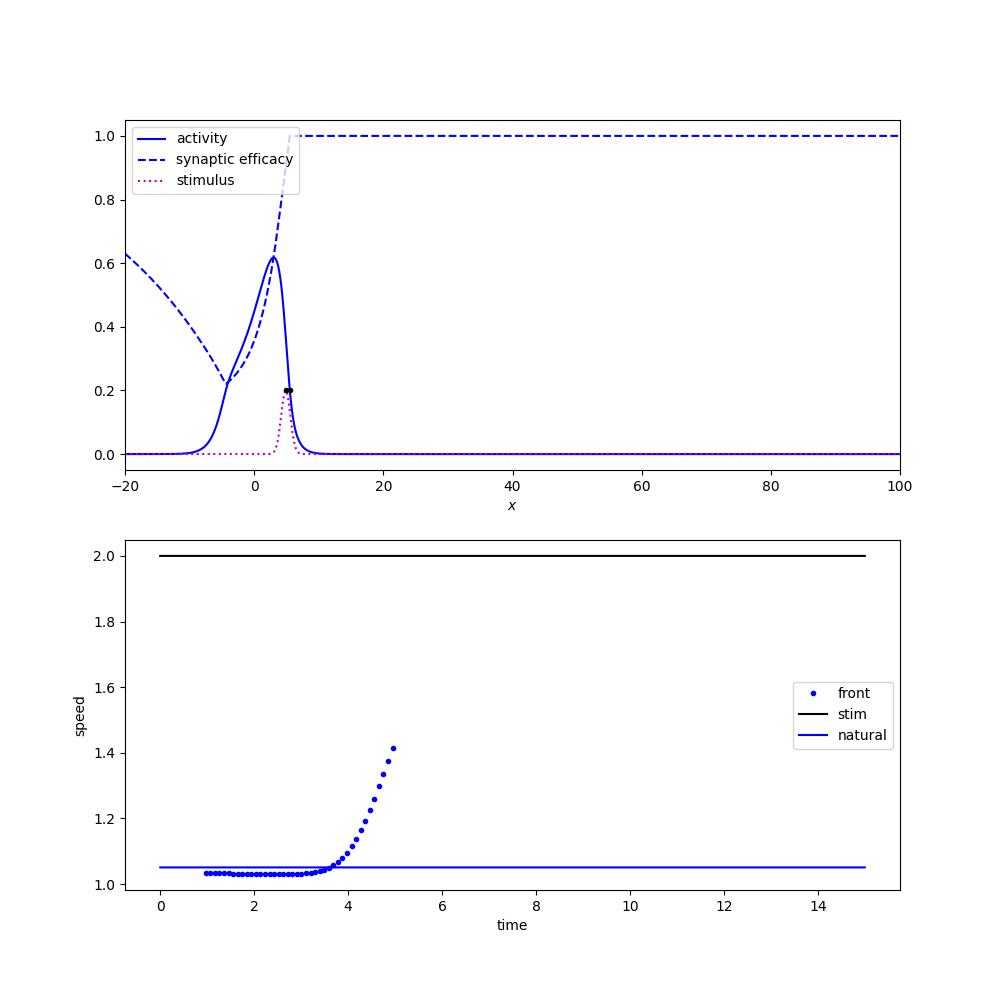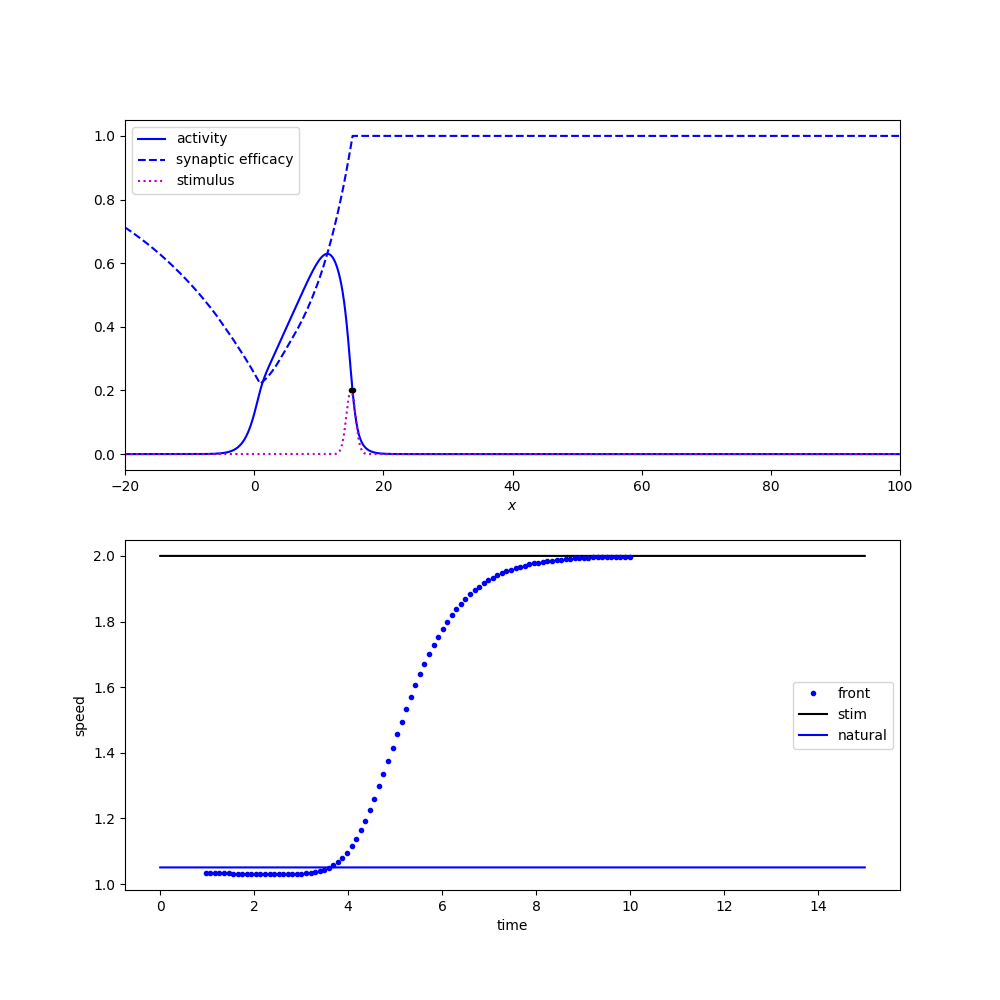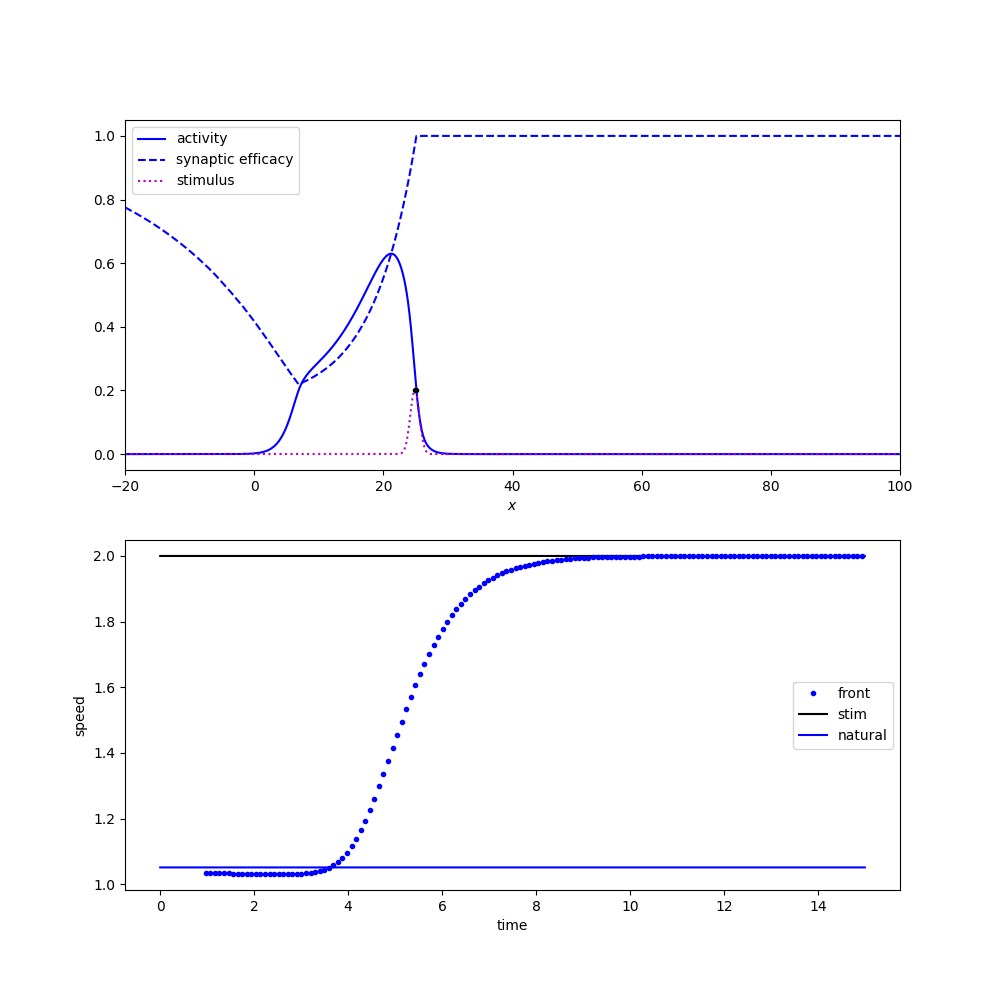
We change the expansion and derive a new wave response. $$ \nu' = -\frac{\langle v_1, I_u(\xi + \varepsilon \nu, t) \rangle + \langle v_2, I_q(\xi + \varepsilon \nu, t) \rangle}{\tau_u \langle v_1, U' \rangle + \tau_q \langle v_2, Q' \rangle} $$

Pulse will entrain if steady-state solutions are stable. Link to derivation.

Next we're working on the apparent motion stimulus.