Time stepping referes techniques that propagate initial condidtions of an ODE or PDE discretely through time to obtain a numerical solution. Presently this article discusses only forward and backward Euler time-stepping.
- Euler Time-Stepping
- Forward Euler Time-Stepping
- Backward Euler Time-Stepping
- Accuracy
- Backward Differentiation Formulae (BDF Schemes)
- BDF2
- References
Grady recommends LeVeque's book [1] - presumably chapter 5 (p. 113).
Euler Time-Stepping
Euler time-stepping is explored in Experiment 001.
Problem
Given the differential equation $\vec{y}^\prime(t) = f(t, \vec{y})$ and the initial condition $\vec{y}_0$ find $\vec{y}(t)$.
We will approximate the true solution with a discrete solution but choosing a step size $\Delta t$, denoting the time at each step as $t_0 +n \Delta t = t_n$, then approximating the solution $\vec{y}_n \approx \vec{y}(t_n)$ at each step. This is done by using forward or backward approximations of $\vec{y}^\prime_n$.
Forward Euler Time-Stepping
In forward Euler we approximate $$\vec{y}^\prime(t) \approx \frac{\vec{y}_{n+1} - \vec{y}_n}{\Delta t}\text{.}$$ Using the definition of our differential equation we obtain the recurrence relation $\vec{y}_{n+1} = \vec{y}_n + \Delta t f(t_n, \vec{y}_n)$. This relation gives the next time-step explicitly in terms of the previous.
Stability
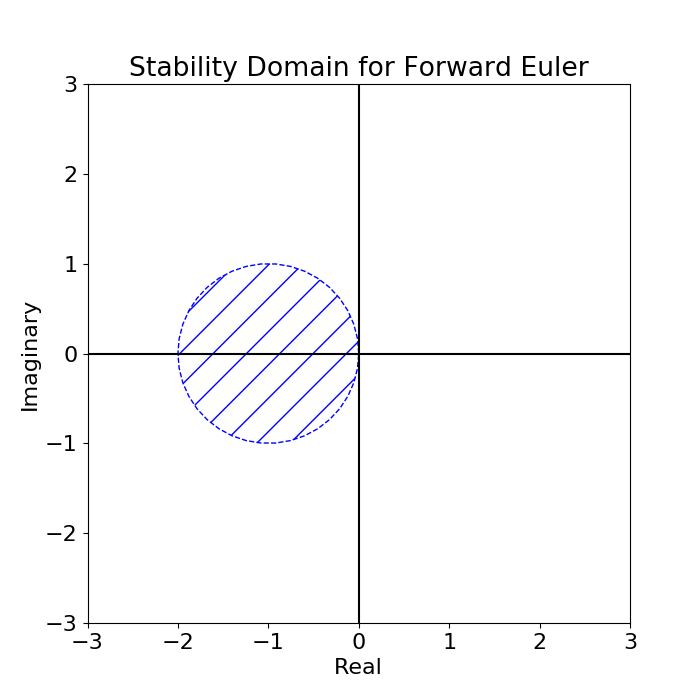
In analyzing the stability we first consider the one dimensional linear case where $f(t, y) = \lambda y$. Our forward formulation can now be expressed as $y_{n+1} = (1+\lambda \Delta t)y_n$ which leads to the solution $$ y_n = (1+\lambda \Delta t)^n y_0 $$ by induction.
This soultion is stable if $\norm{1+\lambda \Delta t}<1$. The stability domain is depicted in the picture to the right.
Backward Euler Time-Stepping
In backward Euler we approximate $$\vec{y}^\prime(t) \approx \frac{\vec{y}_{n} - \vec{y}_{n-1}}{\Delta t}\text{.}$$ Using the definition of our differential equation we obtain the recurrence relation $\vec{y}_{n+1} = \vec{y}_n + \Delta t f(t_n, \vec{y}_{n+1})$. This relation gives the next time-step implicitly in terms of the previous.
In the case where $f$ is linear we say $f(t_n, \vec{y}_n) = L\vec{y}_n$. Then the recurrence relation can be expressed explicitly and solved to give $$ \vec{y}_{n} = (I - \Delta t L)^{-n}\vec{y}_0 .$$
Stability
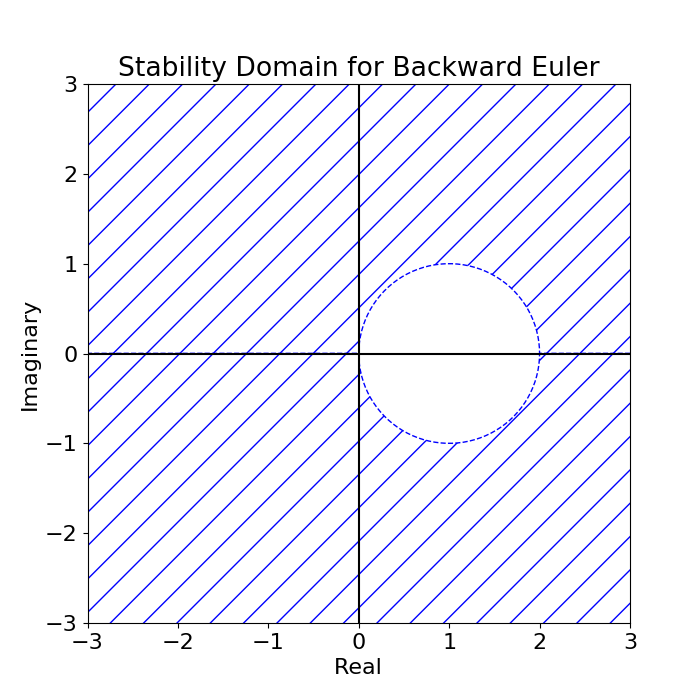
In analyzing the stability we first consider the one dimensional linear case where $f(t, y) = \lambda y$. The solution to the resulting recurrance relation is $y_{n} = \left( \frac{1}{1 - \lambda \Delta t} \right) ^{n}y_0$
This soultion is stable if $\norm{1-\lambda \Delta t}>1$.
For higher dimensional linear systems we have the relation $\vec{y}_{n+1} = (I - \Delta t L)^{-1}\vec{y}_n$ with the corresponding solution $\vec{y}_{n} = (I - \Delta t L)^{-n}\vec{y}_0$. If we perform a spectral decomposistion on the matrix $I - \Delta t L = U \Lambda U^{-1}$ we can reformulate the recurrance relation as $$ \begin{align} \vec{y}_{n+1} &= (I - \Delta t L)^{-1}\vec{y}_n \\ & = U \Lambda^{-1} U^{-1} \vec{y}_n \\ U^{-1} \vec{y}_{n+1} &= \Lambda^{-1} U^{-1} \vec{y}_n \\ \vec{w}_{n+1} &= \Lambda^{-1} \vec{w}_n \end{align} $$ where $\vec{w}_n = U^{-1}\vec{y}_n$. The solution is now represented as a completely decoupuled system. The original system is stable if each of the decoupled relations is stable. That is if $\norm{1-\lambda_i \Delta t}>1$ for $i=1, 2,..., n$ where $\lambda_i$ represents the $i$th eigenvalue of $L$.
Accuracy
The error for a single time step is $\mathcal{O}(\Delta t^2)$. The error at a given time $t = n\Delta t$ where $n$ increases so that $t$ is held constant is given by $\mathcal{O}(\Delta t)$. See Experiment 001 for details.
Backward Differentiation Formulae (BDF Schemes)
Backward Differentiation Formulae are a generalization of Backward Euler. Backward Euler is the simplest BDF scheme and is order $\mathcal{O}(\Delta t^1)$ for a given target time and thus it is denoted BDF1. More generally the formula $\vec{y}_{n+1} = \vec{y}_n + \Delta t f(t_n, \vec{y}_{n+1})$ can be seen as comming from the the Taylor series $$ y(t_0 + \Delta t) = y(t_0) + \Delta t y^\prime(t_0) + \mathcal{O}(\Delta t^2) $$ where it is a second order accurate approximation. After $n \propto \frac{1}{\Delta t}$ steps the accuraccy is $\mathcal{O}(\Delta t)$, thus BDF1.
BDF2
In a similar way, BDF2 is a second order method. It can be derived using Taylors theorem as follows.
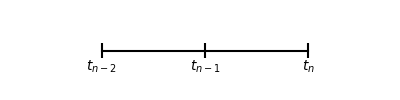
Let $t_{n-2}, t_{n-1}$ and $t_{n}$ denote three sequential time values separated by steps of size $\Delta t$ (illustrated above). Further let $u_n$ denote $u(t_n)$, the function value at time $t_n$. Two results follow from Taylors theorem: $$ \begin{align} u_{n-1} &= u_n -\Delta t u_n^\prime + \frac{\Delta t^2}{2} u_n^{\prime\prime} + \mathcal{O}(\Delta t^3) \\ u_{n-2} &= u_n -2\Delta t u_n^\prime + 2\Delta t^2 u_n^{\prime\prime} + \mathcal{O}(\Delta t^3) \end{align} $$ Multiplying the first equation by $-4$ and adding it to the second we obtain $$ u_{n-2} - 4 u_{n-1} = -3 u_n + 2 \Delta t u_n^\prime + \mathcal{O}(\Delta t^3) $$ and then it follows that a second order accurate approximation to $\Delta t u_n^\prime$ is given by $$ \Delta t u_n^\prime = \tfrac{3}{2}u_n - 2u_{n-1} + \tfrac{1}{2}u_{n-2}. $$ When this is applied to PDEs dicretized in space we approximate $u_n^\prime \approx L u_{n}$. Thus we arrive at the two step reccurance relation $$ \vec{u}_{n} = \left( \tfrac{3}{2}I - \Delta t L \right ) ^{-1} (2\vec{u}_{n-1} - \tfrac{1}{2}\vec{u}_{n-2}). $$
Stability
Similarly to BDF1, BDF2 is stable if $\norm{\tfrac{3}{2}-\lambda \Delta t}>1$ for every $\lambda$ that is an eigenvalue of $L$.
References
- Randall J. LeVeque. Finite Difference Methods for Ordinary and Partial Differential Equations. SIAM, 2007. URL: https://epubs.siam.org/doi/book/10.1137/1.9780898717839, doi:10.1137/1.9780898717839.fm.
