$\newcommand{\norm}[1]{\left\lVert#1\right\rVert} \newcommand{\sint}{\text{s}\kern-5pt\int} \newcommand{\powerset}{\mathcal{P}} \newcommand{\RR}{\mathbb{R}} \newcommand{\NN}{\mathbb{N}} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\CC}{\mathbb{C}} \newcommand{\SS}{\mathbb{S}} \newcommand{\MM}{\mathbb{M}} \renewcommand{\Re}{\operatorname{Re}} \renewcommand{\Im}{\operatorname{Im}} \renewcommand{\vec}[1]{\mathbf{#1}}$

Radial Basis Function
Authors: Sage Shaw
Wed Oct 17 14:57:49 2018

This article defines radial basis fuctions (RBFs), describes several types of RBF, and discusses their motivation and applications.

  1. Definition
  2. Examples
    1. Shape Parameter RBFs
    2. Polyharmonic Spline RBFs
    3. Compactly Supported RBFs
  3. History
  4. References

Definition

The definition of radial basis functions is best understood through (and motivated by) the context of interpolation. The Mairhuber-Curtis theorem [1][2] suggests that basis functions that do not depend on the sample points will be unreliable. Choosing radialy symmetric basis functions centered at the sample points avoids this.

Definition: Radial Kernel and Radial Function
A radial function is a function on the radius: $\phi: [0, \infty) \to \RR$. When a radial function is paired with a metric on a vector space $\norm{\cdot}: V \to [0, \infty)$ the function $\phi_\vec{c}: V \to \RR$ defined by $\phi_\vec{c}(\vec{x}) = \phi(\norm{\vec{x} - \vec{c}})$ is said to be a radial kernel centered at $\vec{c} \in V$. For a set of distinct points in the domain $\{\vec{x}_i\}_{i=1}^n$ the radial kernels $\{\phi_{\vec{x}_i} \}_{i=1}^n$ are said to be radial basis functions if they are linearly independent (they are a basis for their span).

If we wish to interpolate a function at a set of points then a set of radial kernels centered at those points may not be a valid basis. For example, the function $\phi(r)=r^2$ is a perfectly valid radial function but in one dimension using the standard euclidian distance, the set of functions $\{x^2, (x-1)^2, (x-2)^2, (x-3)^2\}$ are linearly dependent and thus can't be basis functions. More generally, one can guarantee a nonsingular interpolation matrix by criteria on the radial function.

Definition: Completely Monotone Function[3]
A function $\psi: [0, \infty) \to \RR$ is said to be completely monotone if
  1. $\psi \in C[0, \infty)$
  2. $\psi \in C^\infty (0, \infty)$
  3. $(-1)^k \frac{d^k \psi}{dt^k}(t) \geq 0$ for $t>0$ and $k = 0, 1, 2, \dots$

Completely Monotone radial functions have desireable properites for the purposes of interpolation (and by extension RBF-FD).

Michelli's Theorm[4]
Let $\{\vec{x}_i\}_{i=1}^n \subseteq X$, an inner product space. Let $\psi$ be a continuous radial kernel. Definie the matrix $A_{ij} = \psi \left( \norm{\vec{x}_i - \vec{x}_j}^2 \right)$. If $\psi'$ is non-constant and completely monotone on $(0, \infty)$ then $A$ is non-singular.

When our radial function is completely monotone Michelli's theorm proves that the RBf interpolation matrix will be non-singular.

Examples

The original radial function used by Hardy [5] is the multiquadric $$ \phi(r) = \sqrt{1 + (\varepsilon r)^2}. $$ Since then many other good choices for radial functions have been discovered.

Shape Parameter RBFs

The multiquadric mentioned above has a parameter $\varepsilon$ known as the shape parameter. Generally speaking, as $\varepsilon \to 0$ the graph approaches a flat line as seen in the plot of the Gaussian below.

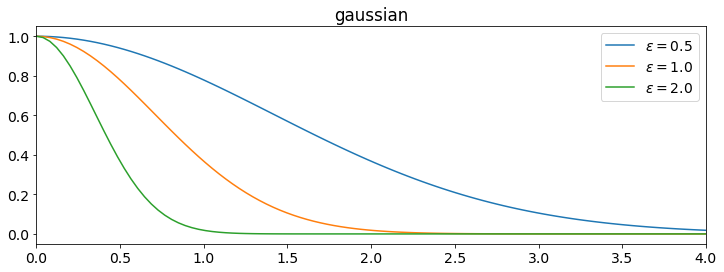
The following are a list of some shape-parameter RBFs used in practice. All satisfy Michelli's theorem above. \begin{align*} \textbf{Gaussian - } \phi(r)&= e^{-(\varepsilon r)^2} \\ \textbf{Multiquadric - } \phi(r)&= \sqrt{1 + (\varepsilon r)^2} \\ \textbf{Inverse Multiquadric - } \phi(r)&= \frac{1}{\sqrt{1 + (\varepsilon r)^2}} \\ \textbf{Inverse Quadratic - } \phi(r)&= \frac{1}{1+(\varepsilon r)^2} \\ \end{align*}

Polyharmonic Spline RBFs

Polyharmonic splines can be seen as a generalization of the cubic and thin-plate splines. In fact there are particular boundary conditions on cubic splines that are equivalent to RBF interpolation using $\phi(r)=r^3$ [6]. The cubic splines are of this form \begin{align*} \phi(r) & = r^{2k+1} \text{ for } k \in \NN \\ \phi(r) & = r^{2k}\log(r) \text{ for } k \in \NN \\ \phi(r) & = r^3 &\text{(cubic spline - special case)} \\ \phi(r) & = r^{2}\log(r) &\text{(thin-plate spline - special case)} \\ \end{align*}

Generally PHS RBFs have lower orders of convergence than shape parameter RBFs, however this can be remedied by adding a few low degree polynomials to the basis.

Compactly Supported RBFs

History

References

  1. John C. Mairhuber. On haar's theorem concerning chebychev approximation problems having unique solutions. Proceedings of the American Mathematical Society, 7(4):609–615, 1956. URL: http://www.jstor.org/stable/2033359.

  2. Jr. Philip C. Curtis. N-parameter families and best approximation. Pacific Journal of Mathematics, 9(4):1013–1028, 1959. URL: https://msp.org/pjm/1959/9-4/pjm-v9-n4-p04-s.pdf.

  3. E. Ward Cheney and William A. Light. A Course in Approximation Theory (The Brooks/Cole Series in Advanced Mathematics). Brooks Cole, 1999. ISBN 0534362249.

  4. Charles A. Micchelli. Interpolation of scattered data: distance matrices and conditionally positive definite functions. Constructive Approximation, 2(1):11–22, Dec 1986. URL: https://doi.org/10.1007/BF01893414, doi:10.1007/BF01893414.

  5. Rolland L. Hardy. Multiquadric equations of topography and other irregular surfaces. Journal of Geophysical Research, 76(8):1905–1915, 1971. URL: https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/JB076i008p01905, arXiv:https://agupubs.onlinelibrary.wiley.com/doi/pdf/10.1029/JB076i008p01905, doi:10.1029/JB076i008p01905.

  6. B Fornberg, T A Driscoll, G Wright, and R Charles. Observations on the behavior of radial basis functions near boundaries. Comput. Math. Appl., 43:473–490, 2002. URL: https://math.boisestate.edu/~wright/research/rbf_paper_final.pdf.