Approximating the effect of inputs and cortical geometry on wave propagation in neural fields
Sage Shaw - University of Colorado Boulder, USA
May 9th, 2025
Mathematical Models of Neural Encodings
Outline
- Neural Field Models
- One Dimension
- Stimulus response
- Entrainment
- Two Dimension
- Numerical Analysis: the Projection Method
- RBF-QF method-of-lines solver for neural fields
- Curvature showcase
- Future Work
Neural Field Models
Biological Neural Networks
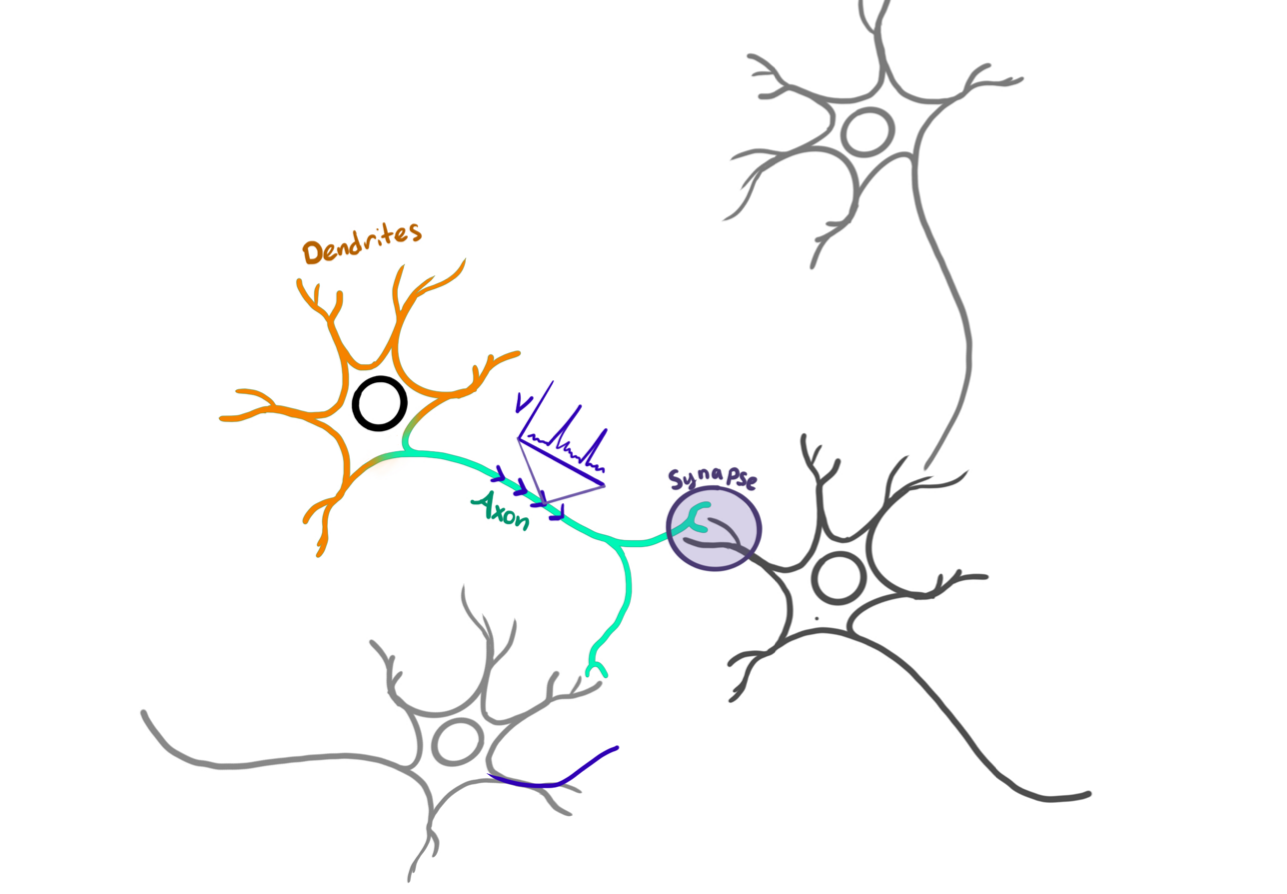
Image courtesy of Heather Cihak.
Neural Field Models
- Organize neural populations on a line
- Connectivity is determined by distance
- Extend to a continuum limit
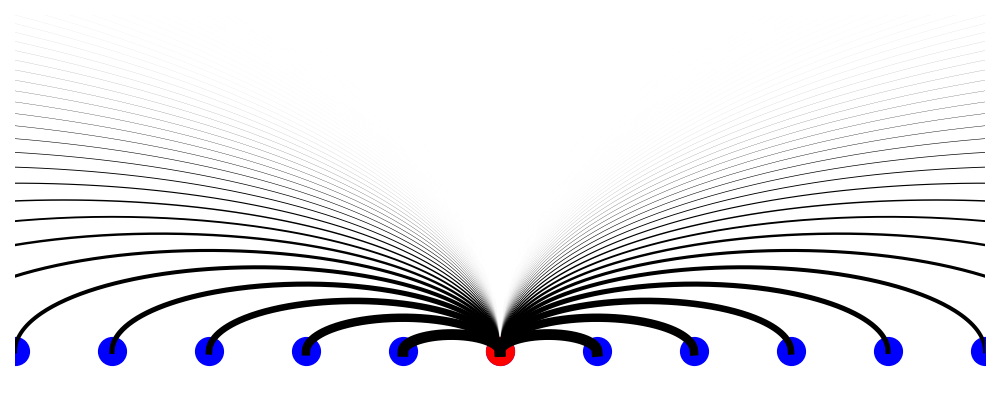
Model
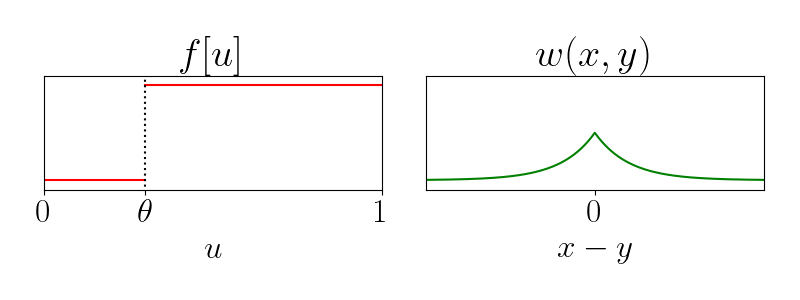
\begin{align*} \tau_u \frac{\partial}{\partial t}\underbrace{u(t, x)}_{\text{Activity}} &= -u + \underbrace{ \int_\Omega \color{green}{w}(x, y) \quad \color{red}{f}[u(t, y)] \ d y}_{\substack{\text{network}\\\text{stimulation}}} \\ \end{align*}
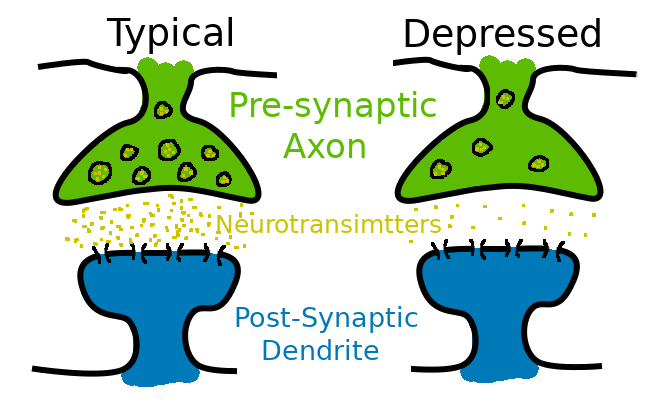
Synaptic Depression
Rapid firing depletes pre-synaptic resources.
Model with Synaptic Depression
\begin{align*} \tau_u \frac{\partial}{\partial t} u(t, x) &= -u + \int_\Omega w(x, y) \quad \color{blue}{q}(y) \quad f[u(t, y)] \ d y \\ \underbrace{\tau_q}_{\text{slow}} \frac{\partial}{\partial t}\underbrace{q(x,t)}_{\substack{\text{Synaptic}\\\text{Efficacy}}} &= 1 - q - \underbrace{\beta}_{\substack{\text{rate of}\\\text{depletion}}} q \underbrace{f(u)}_{\substack{\text{firing-rate}\\\text{function}}} \end{align*}
1D Neural Fields
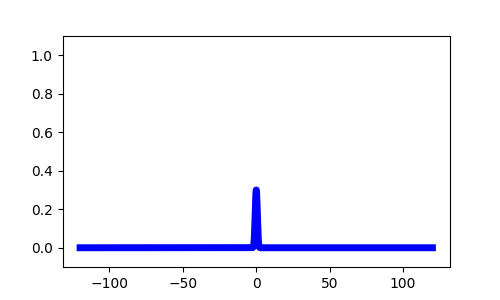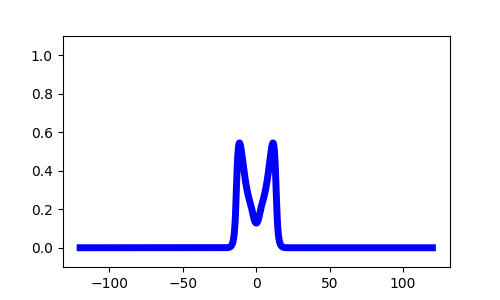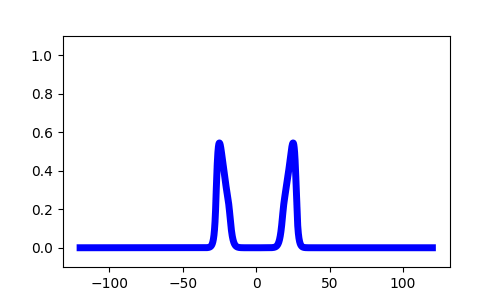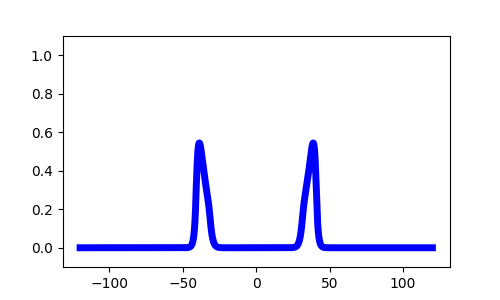
Pulse solutions if
$\frac{1}{1+ \beta} < \theta$Stimulus Response
Correcting Position
- Position encoded as a pulse
- Must be corrected
Localized Pulse Stimulus
Asymptotic Approximation
add stimulus terms $$ \begin{align*} \tau_u u_t &= -u + w * (q f[u]) + \varepsilon I_u(x, t) \label{eqn:forced_u} \\ \tau_q q_t &= 1 - q - \beta q f[u] + \varepsilon I_q(x, t) \label{eqn:forced_q} \end{align*} $$substitute with the expansion $$ \begin{align*} u(\xi, t) &= U\big( \xi - \varepsilon \nu(t) \big) + \varepsilon \phi\big(\xi - \varepsilon \nu(t), t\big) + \mathcal{O}(\varepsilon^2) \\ q(\xi, t) &= Q\big( \xi - \varepsilon \nu(t) \big) + \varepsilon \psi\big(\xi - \varepsilon \nu(t), t\big) + \mathcal{O}(\varepsilon^2) \end{align*} $$
Stimulus Response Function
$$ \frac{\partial}{\partial t}\nu = \frac{ \langle v_1 ,I_u(\xi + \color{blue}{\varepsilon \nu}, t)\rangle + \langle v_2, I_q(\xi +\color{blue}{\varepsilon \nu}, t)\rangle }{\underbrace{-\tau_u \langle v_1, U' \rangle - \tau_q \langle v_2, Q' \rangle}_{K}} $$Stimulus Response
Entrainment
Tracking a moving stimulus
Tracking a moving stimulus
Entraining to a moving stimulus
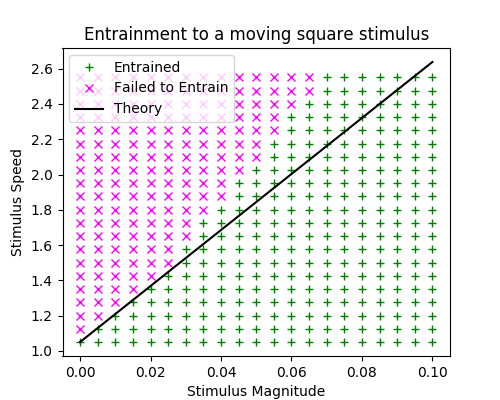
Asymptotic threshold
$$ \Delta_c \lt \varepsilon \frac{c\tau_u}{K}$$
Asymptotic Entrainment Threshold
$ \Delta_c < \varepsilon \frac{c\tau_u}{K} \color{green}{\frac{T_\text{on}}{T_\text{on} + T_\text{off}}} $
Numerical Analysis
The Projection method
Neural Field Model
$\partial_t \color{blue}{u}(t, \vecx) = -\color{blue}{u} + \int_{\Omega} \color{green}{w}(\vecx, \vecy) \color{red}{f}[\color{blue}{u}(\vecy)] d \vecy$
Recreation of Coombes et al. (2012)
- $\color{blue}{u}(t, \vecx)$ - Activity
- $\color{green}{w}(\vecx, \vecy)$ - Connectivity kernel
- $\color{red}{f}[\color{blue}{u}]$ - non-linear firing rate function
Projection Method (Avitabile 2023)
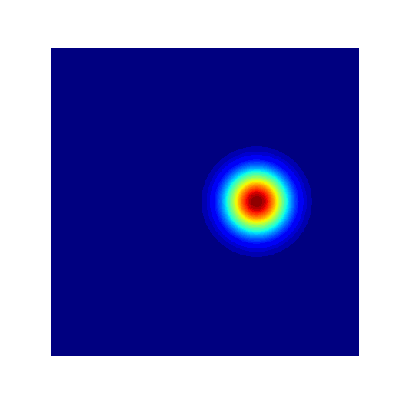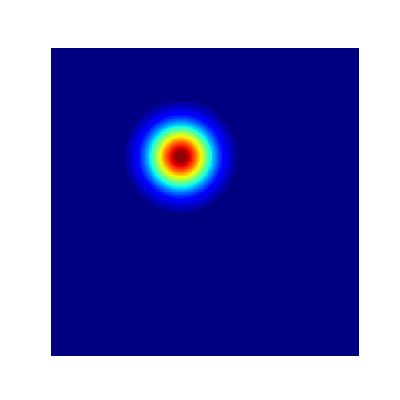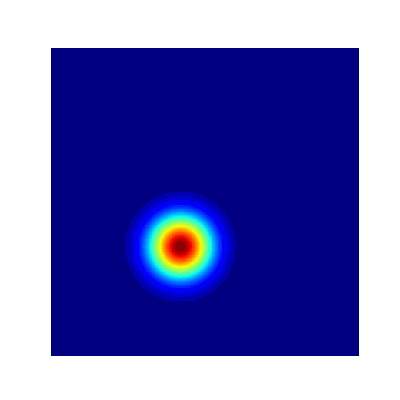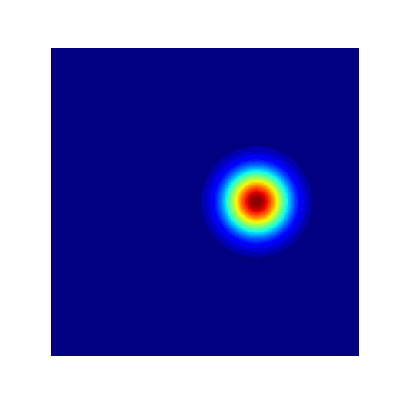
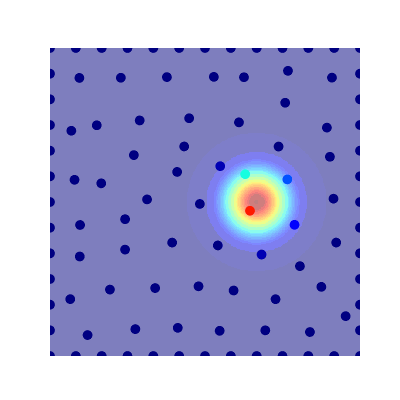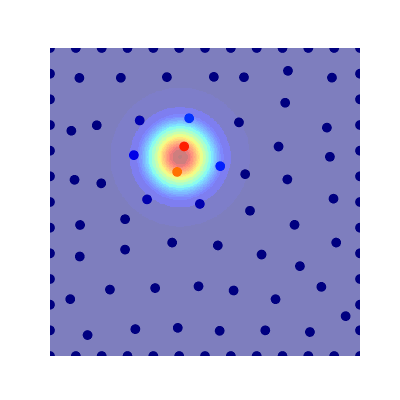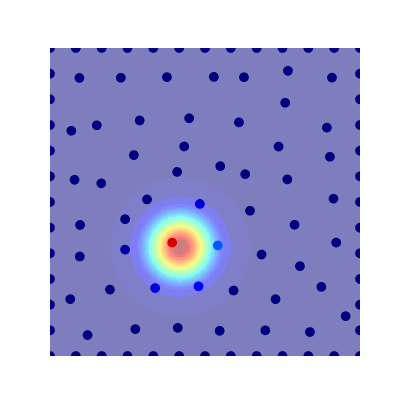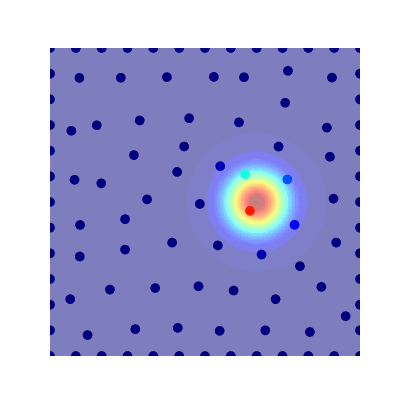
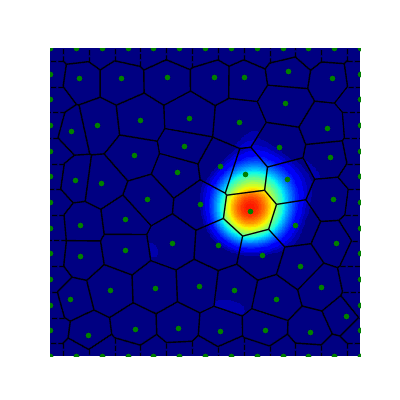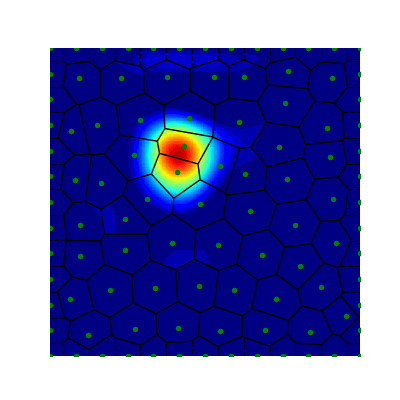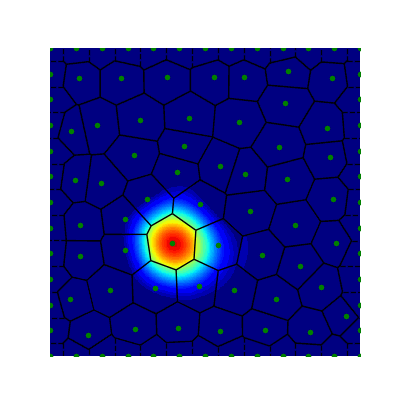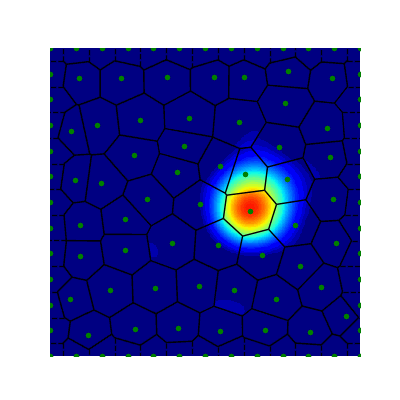
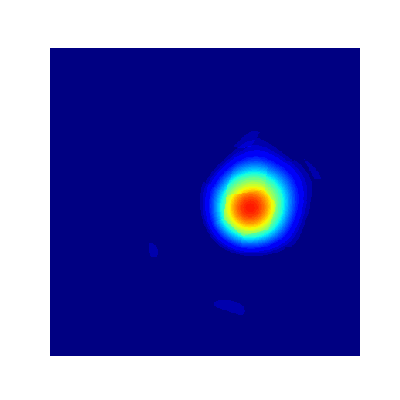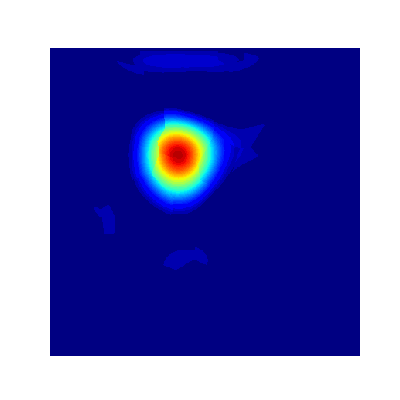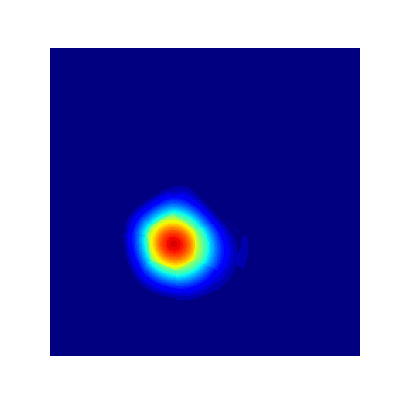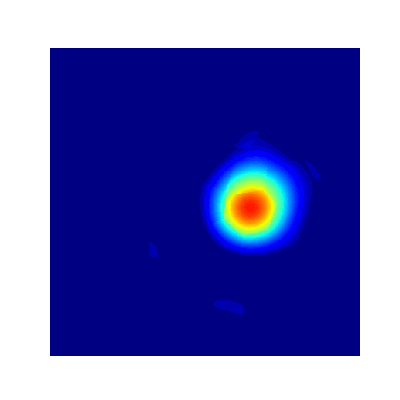
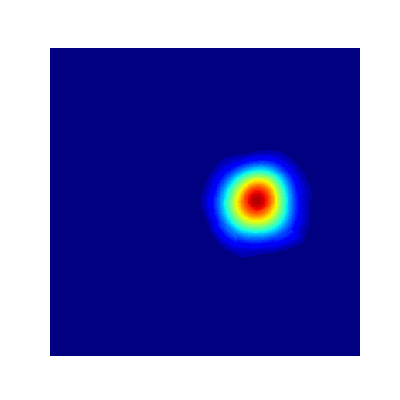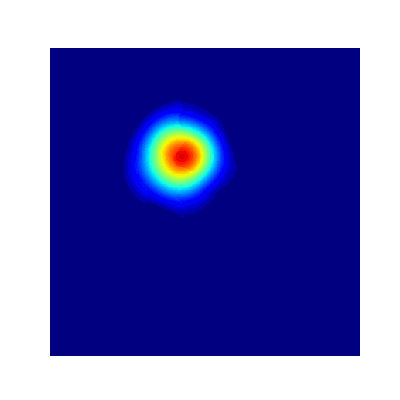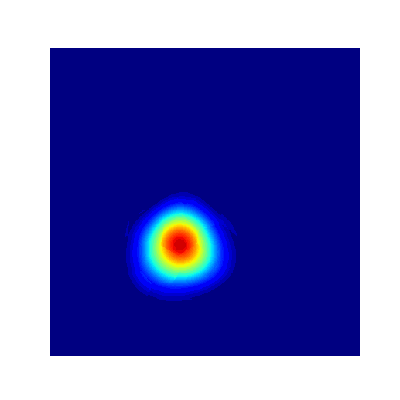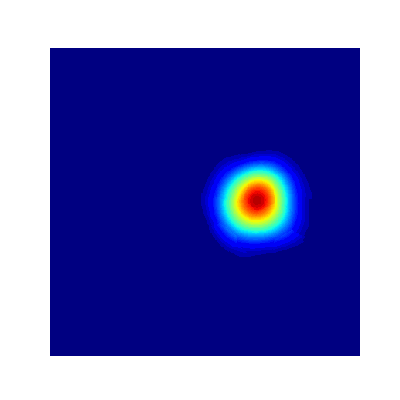
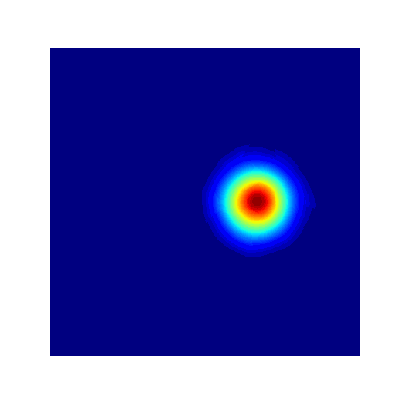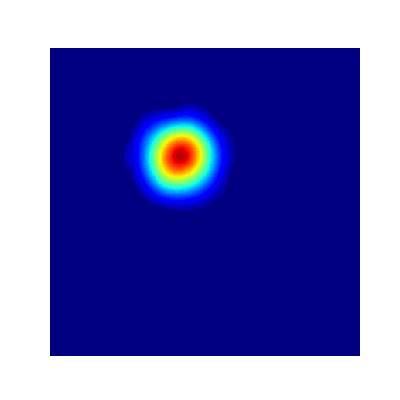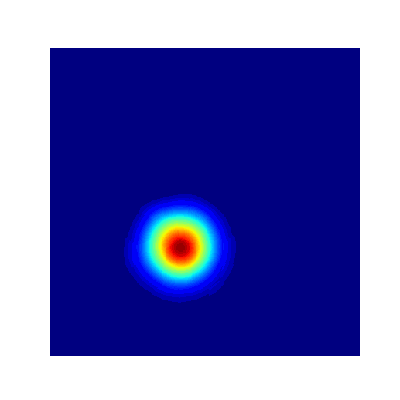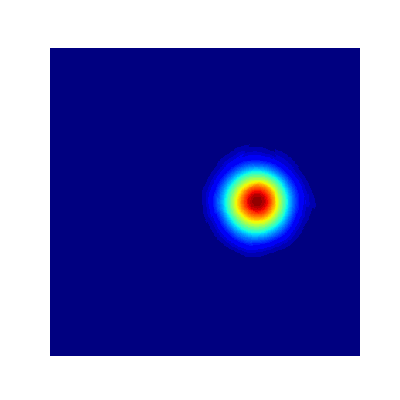
- True Solution
- Collocation
- Projection
- Error
- Projection
- Quadrature
- Time Integration
- $\text{Error} \sim \mathcal{O}(n^{-\text{order}/\text{dim}})$
RBF-QF method-of-lines neural field solver
Radial Basis Function Quadrature Formulae (RBF-QF)
- Given a set of points $\{\vecx_i\} \subset \Omega$
- find weights $\{w_i\}$
- such that $\int_\Omega f \approx \sum w_i \ f(\vecx_i)$
RBF-QF Algorithm


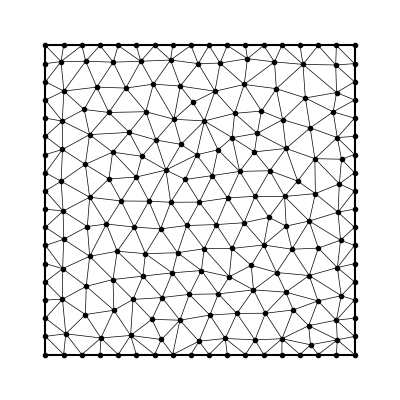
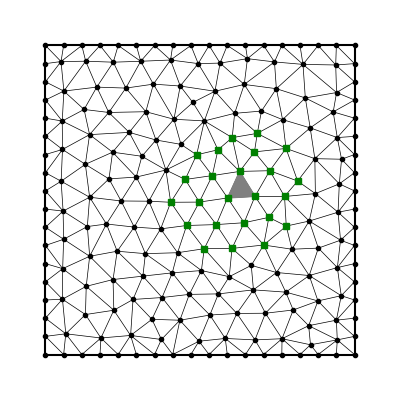
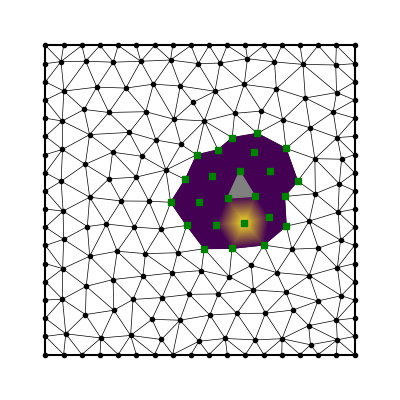
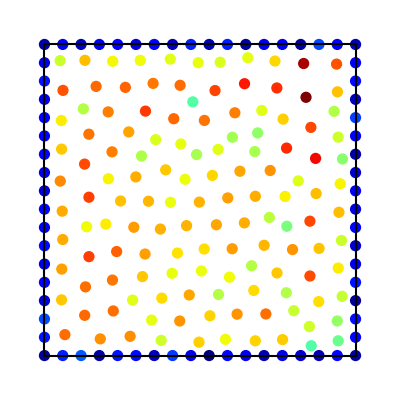
- choose quadrature nodes
- partition domain
- choose stencils
- integrate RBF interpolant
- sum over stencil and elements
The brain is not flat!
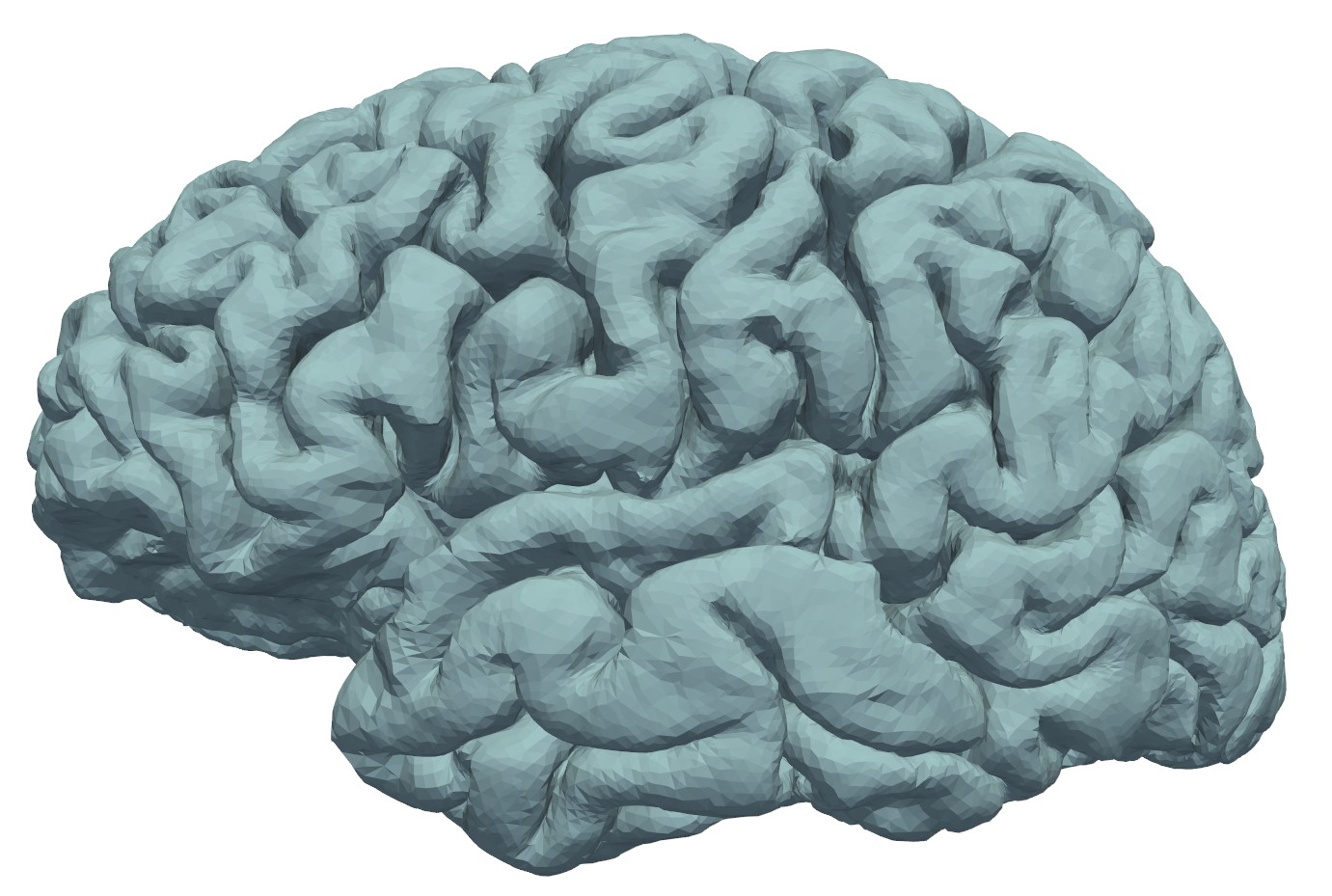
Extending to Manifolds




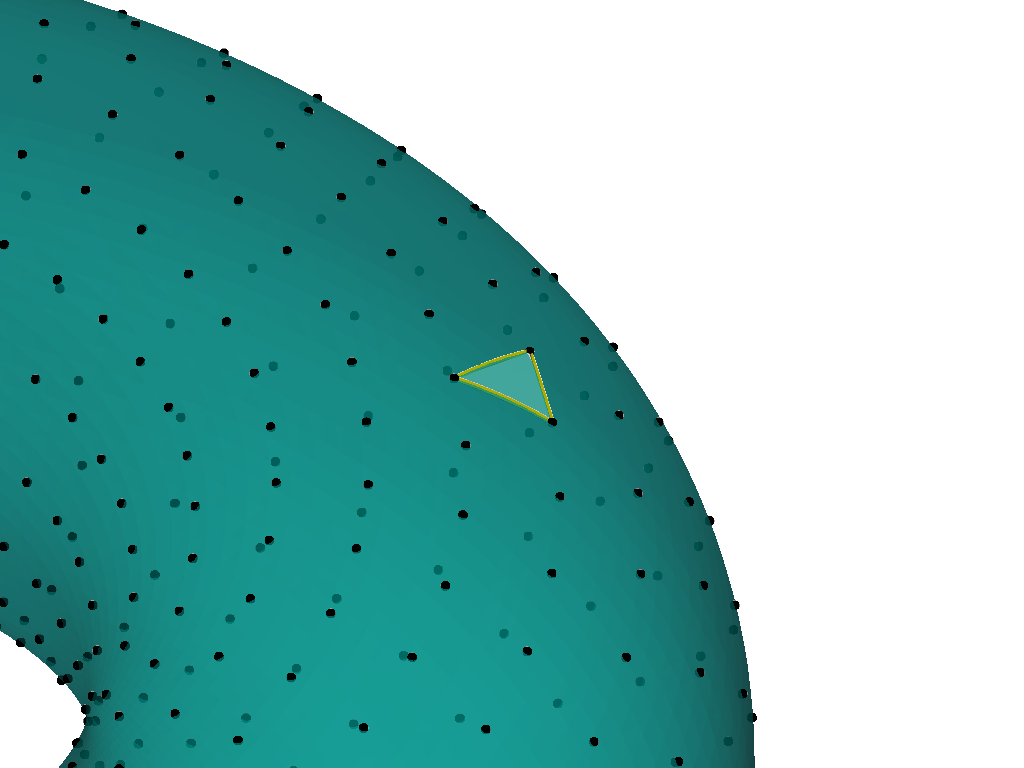
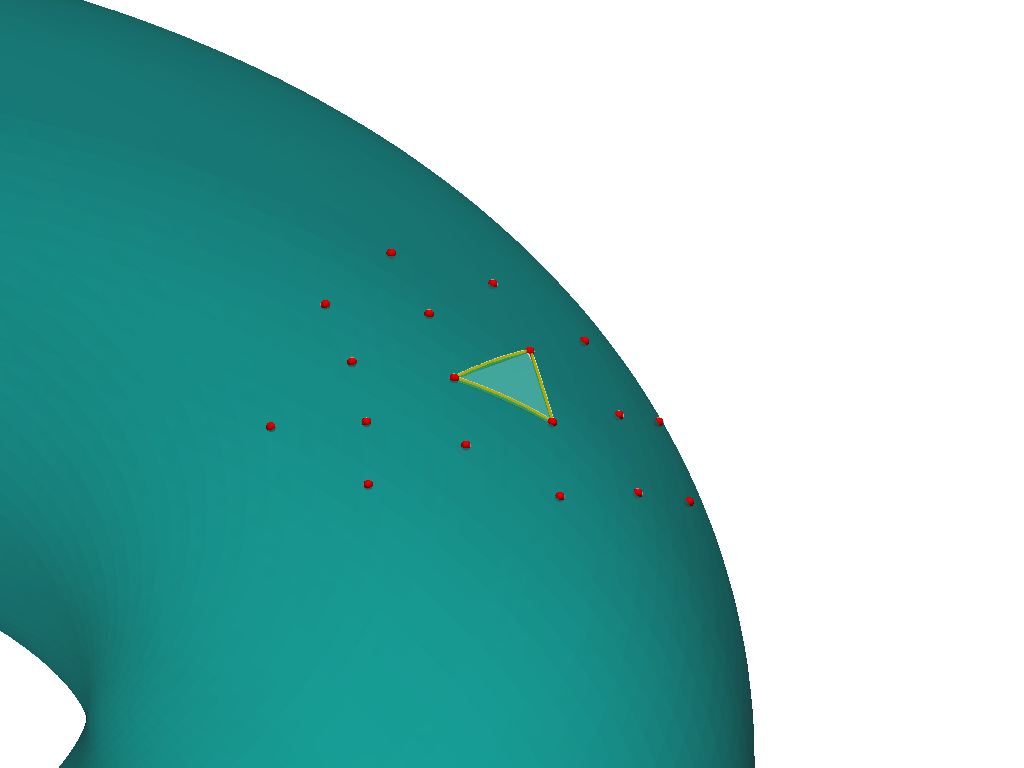
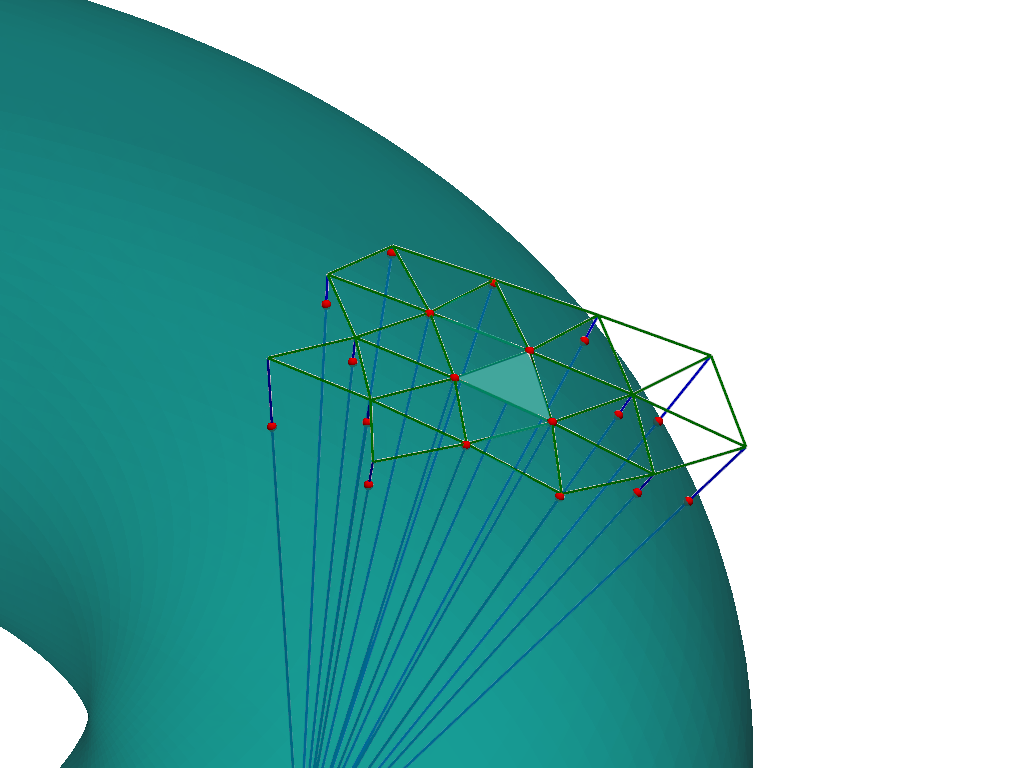
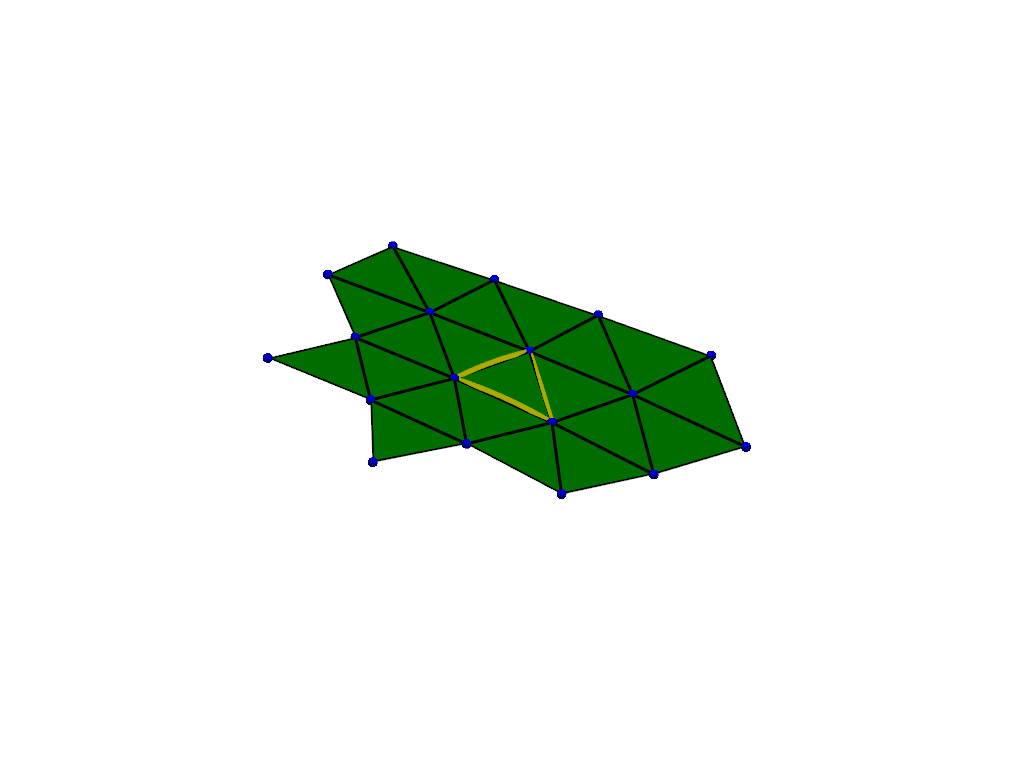
Curvature Showcase
Curvature affects the trajectory
Future Work
Spreading Depression
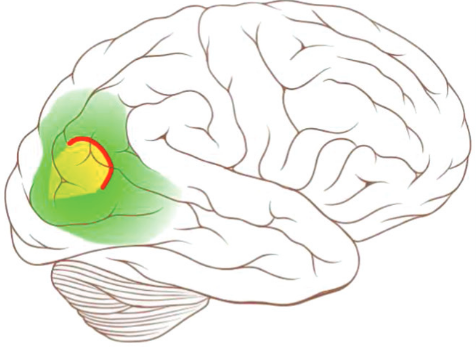
Zandt, Haken, van Putten, and Dahlem (2015)
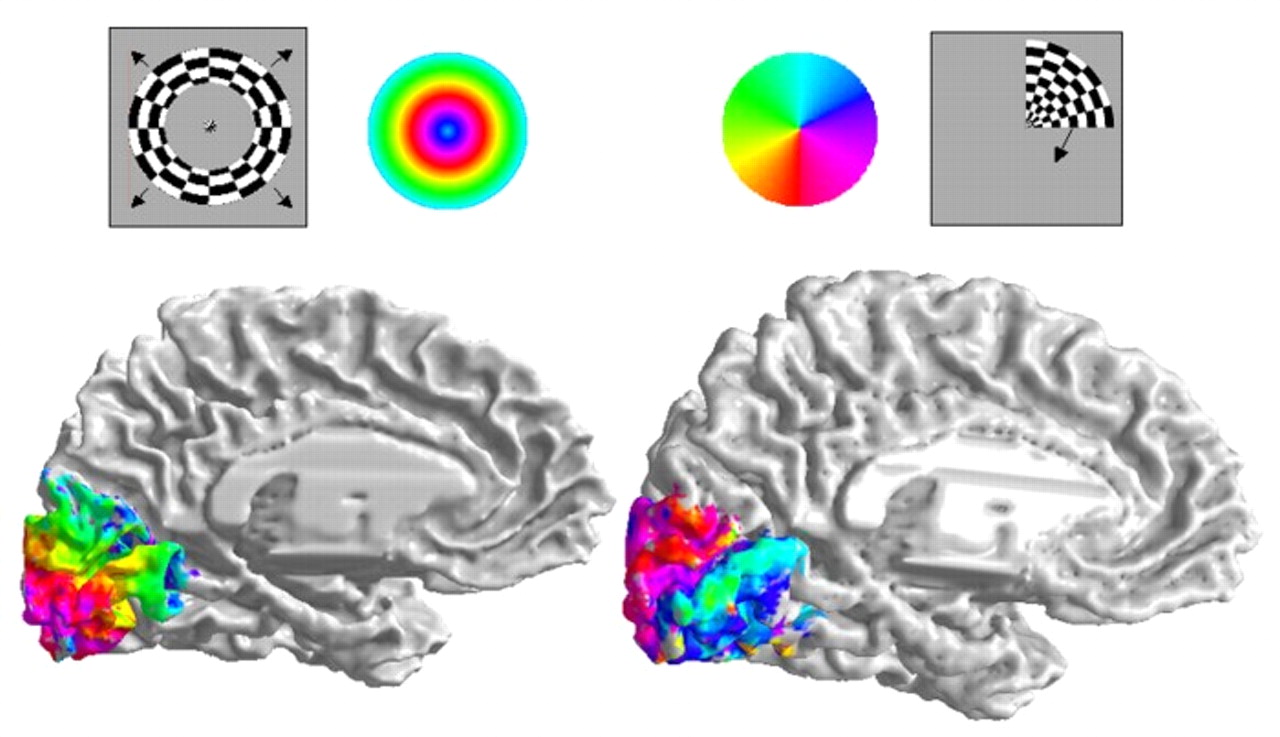
Retinotopic Map
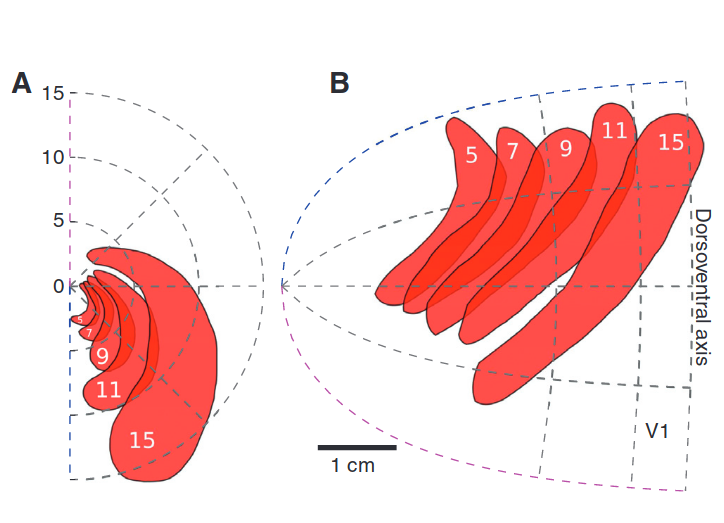
Zandt, Haken, van Putten, and Dahlem (2015)
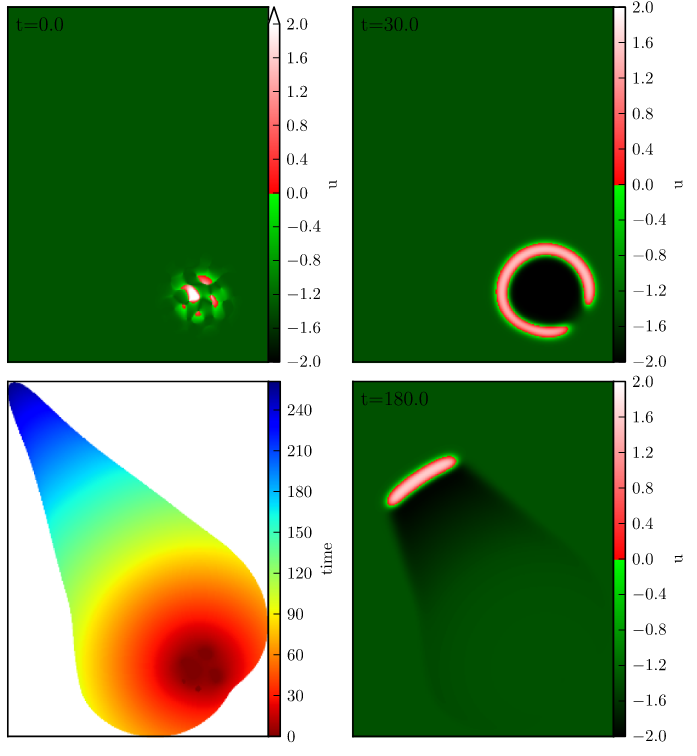
Scintillating Scotoma

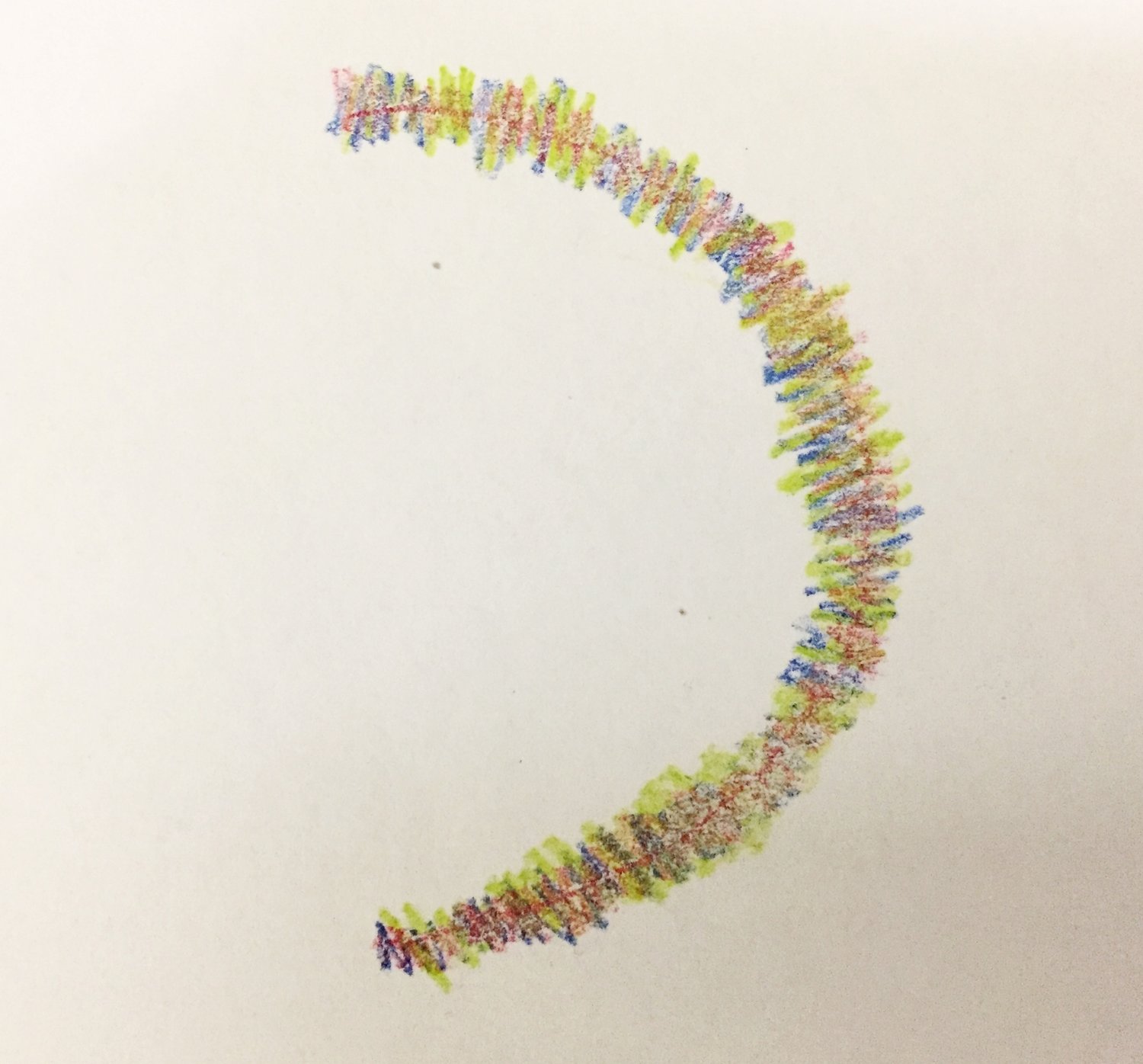

Coupled neural field and diffusion equation
$$\begin{align*} v_t &= -v + w \ast s_p(v, k) + g_v \\ k_t &= \delta k_{xx} + g_k(s, s_p, a, b) + I \end{align*}$$- Neural field model
- Coupled potassium concentration
- Models both ignition and propagation of CSD
A Turing Reaction Diffusion System
$$\begin{align*} u_t &= \delta_u \Delta_{\mathcal{M}} u + \alpha(1-\tau_1 v^2) + v(1-\tau_2 u)\\ v_t &= \delta_v \Delta_{\mathcal{M}} v + \beta(1-\frac{\alpha\tau_1}{\beta} uv) + u(\gamma-\tau_2 v)\\ \end{align*}$$- References
- Funding
- NIH BRAIN 1R01EB029847
- NSF DMS-2207700
Slides:
Auxiliary Slides
Retinotopic Map
Reaction Diffusion on surfaces
$$\begin{align*} u_t &= \underbrace{3u - u^3}_{\text{excitable}} - \underbrace{v}_{\text{recovery}} + \underbrace{D \Delta_{\mathcal{M}}u}_{\text{diffusion}} \\ \frac{1}{\varepsilon} v_t &= u + \beta + K \underbrace{\int_{\mathcal{M}} H(u) \ d \mu_{\mathcal{M}}}_{\text{neurovascular}} \end{align*}$$
- Surface operators: $\Delta_{\mathcal{M}}, \int_{\mathcal{M}} \cdot d \mu_{\mathcal{M}}$
- Curvature affects speed and stability of waves
Coupled neural field and diffusion equation
$$\begin{align*} v_t &= -v + w \ast s_p(v, k) + g_v \\ k_t &= \delta k_{xx} + g_k(s, s_p, a, b) + I \end{align*}$$- Neural field model
- Coupled potassium concentration
- Models both ignition and propagation of CSD
A Turing Reaction Diffusion System
$$\begin{align*} u_t &= \delta_u \Delta_{\mathcal{M}} u + \alpha(1-\tau_1 v^2) + v(1-\tau_2 u)\\ v_t &= \delta_v \Delta_{\mathcal{M}} v + \beta(1-\frac{\alpha\tau_1}{\beta} uv) + u(\gamma-\tau_2 v)\\ \end{align*}$$Radial Basis Funtion Interpolation








- Function to approximate
- Sample at scatterd nodes
- $\phi_j(\vecx) = \Phi(||\vecx - \vecx_j||)$
- $f(\vecx) \approx s(\vecx) = \sum_j c_j \phi_j(\vecx)$
- $\text{Error} \to 0$ as $n \to \infty$
RBF Interpolation Properties
- scattered nodes in any number of dimensions*
- mesh-free*
- arbitrary order of accuracy*
- can be used to find
- finite difference formulae
- quadrature formulae
Radial Basis Function Quadrature Formulae
Experimental Results
Gaussian Test Functions

Gaussian Test Functions


Gaussian Test Functions

Quadrature Convergence

Testing manufactured solution

Convergence

Next Steps
- Adapt to surfaces.
- Incorporate cortical spreading depression (CSD).
- Study the effects of realistic cortical curvature on CSD wave generation and propagation.
Our Contributions
- Neural Field Solver
- High Order Accurate
- Flexible Geometry
- Simplifed Error Analysis
- Adapt to Surfaces
- Couple with CSD

Auxiliary Slides
The Kilpatrick Lab

Prof. Zack Kilpatrick

Dr. Tahra Eissa

Sage Shaw

Noah Parks

Will Magrogan
Reaction Diffusion Model
$$\begin{align*} u_t &= \underbrace{u - \frac{1}{3}u^3}_{\text{excitable}} - \underbrace{v}_{\text{recovery}} + \underbrace{D\nabla^2 u}_{\text{Diffusion}} \\ \frac{1}{\varepsilon} v_t &= u + \beta + \underbrace{K\int H(u) d \Omega}_{\substack{\text{neurovascular}\\\text{feedback}}} \end{align*}$$