Zhenpeng Ge and Quan-Xing Liu - 2021
Foraging behaviours lead to spatiotemporal self-similar dynamics in grazing ecosystems
About Me
- Program: applied math PhD
- Old research: numerical PDEs
- New research: computational neuroscience
Why CSCI 5314?
Plant growth and grazing behaviour

Bottom up model
Sheep eat grass
$\therefore$
More sheep
$\Downarrow$
shorter grass.
Top down model
Short grass attracts sheep
$\therefore$
Shorter grass
$\Downarrow$
more sheep
The PDE model
Variables
- $p(\vec{x},t)$ - Plant density
- $h(\vec{x},t)$ - Herbivore density
- $v(p)$ - Herbivore speed
Speed
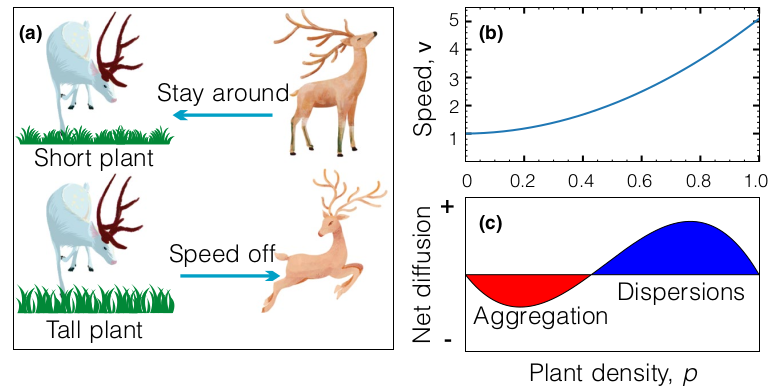
$$v(p) = \alpha p^2 + \beta p + 1$$
$$ p_t = \color{green}{\underbrace{\lambda p(1-p)}_{\text{logistic growth}}} - \color{magenta}{\underbrace{ph}_{\text{predation}}} + \color{lightblue}{\underbrace{\Delta p}_{\text{diffusive spreading}}} $$
$$ h_t = D_0\bigg( \nabla \cdot \color{yellow}{\underbrace{\nabla\big(\overbrace{v^2(p) h}^{\text{2D Brownian motion}} \big)}_{\text{herbivore flux}}} - \color{pink}{\underbrace{\kappa \Delta^2 h}_{\text{correction?}}} \bigg) $$
$\color{pink}{\text{correction}}$? - They cite Tailleur & Cates 2008
Sounds fishy... I think they just added hyper-viscocity to make the finite-differences work.
Simulation
Turring Patters
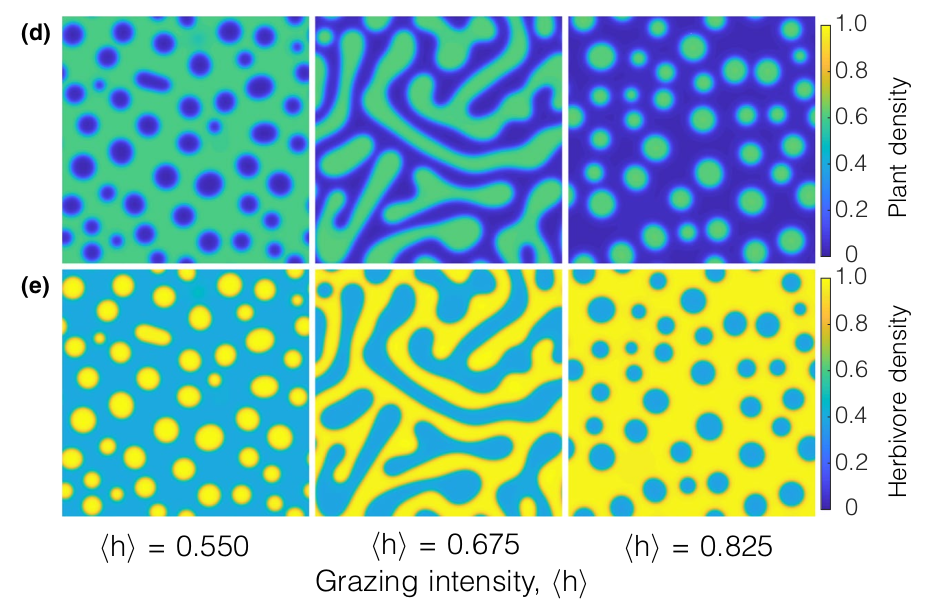
Turring Patters
Parameter Exploration
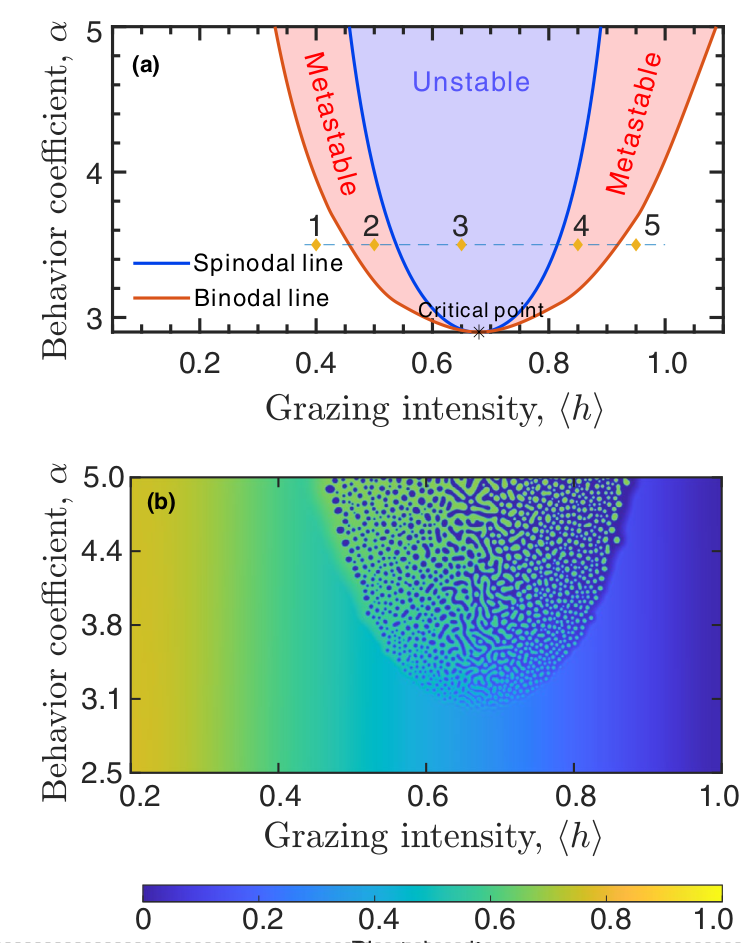
Parameter Exploration
Conclusion
- Impresive coupled model
- You've seen qualitative validation
- They also do some statistical spatiotemporal analysis of patch-size
"Our work suggests that scale-dependent feedback can be coupled with phase-separation systems for spatial self-organization. The traditional view considers scale-dependent feedback and phase separation as two distinct principles that function separately in ecology."
My code: https://tinyurl.com/2p8sz5tt